Trajectories
Isogonal Trajectories
When two curves intersect in a plane, the angle between them is defined to be the angle made by their respective tangents drawn at their point of intersection.
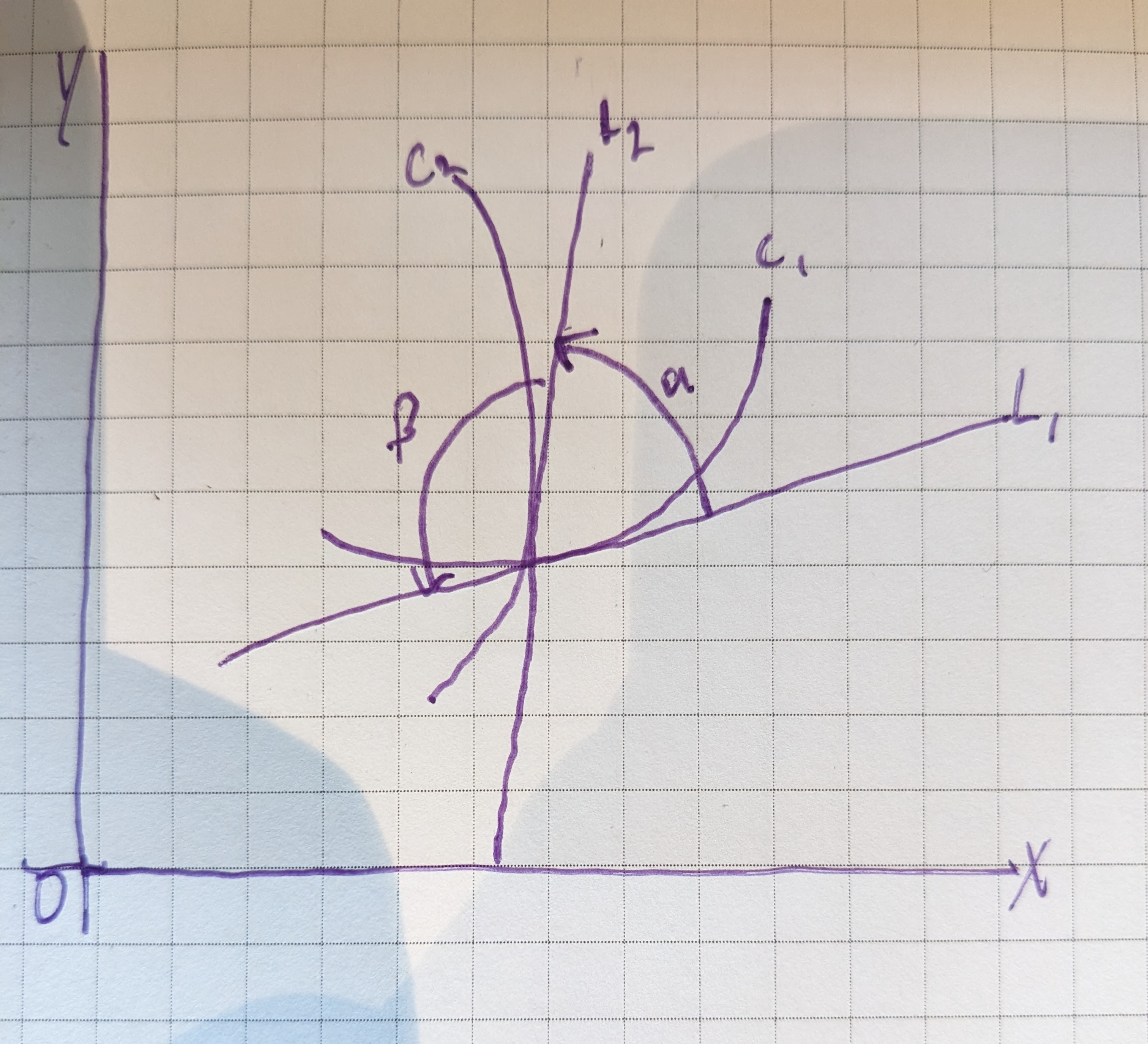
In the above figure, $\alpha$ is the positive angle from the curve $c_1$ with tangent line $L_1$ to the curve $c_2$ with tangent line $L_2$; $\beta$ is the positive angle from the curve $c_2$ to the curve $c_1$. If we call $m_1$ the slope of $L_1$ and $m_2$ the slope of $L_2$, then by a formula in analytic geometry:
$$ \tag{14.11} \tan{\alpha} = \frac{m_2 - m_1}{1+m_1 m_2}; \quad \tan{\beta} = \frac{m_1 - m_2}{1+m_1 m_2}. $$
Definition 14.12 A curve which cuts every member of a given 1-parameter family of curves in the same angle is called an isogonal trajectory of the family.
If we call ${y_1}'$ the slope of a curve of a given 1-parameter family, $y'$ the slope of an isogonal trajectory of the family, and $\alpha$ their angle of intersection measured from the tangent line with slope ${y_1}'$ to the tangent line with slope ${y_1}'$, then by (14.11):
$$ \tag{14.13} \tan{\alpha} = \frac{ {y_1}' - y'}{1+y' {y_1}'} $$
Orthogonal Trajectories
Definition 14.2 A curve which cuts every member of a given 1-parameter family of curves in a $90^\circ$ angle is called an orthogonal trajectory of the family.
Let ${y_1}'$ be the slope of a give nfamily and let $y'$ be the slope of an orthogonal family. Then, by a theorem in analytic geometry:
$$ \tag{14.21} {y_1}' y' = -1,~y' = - \frac{1}{ {y_1}'} $$
Orthogonal Trajectories in Polar Coordinates
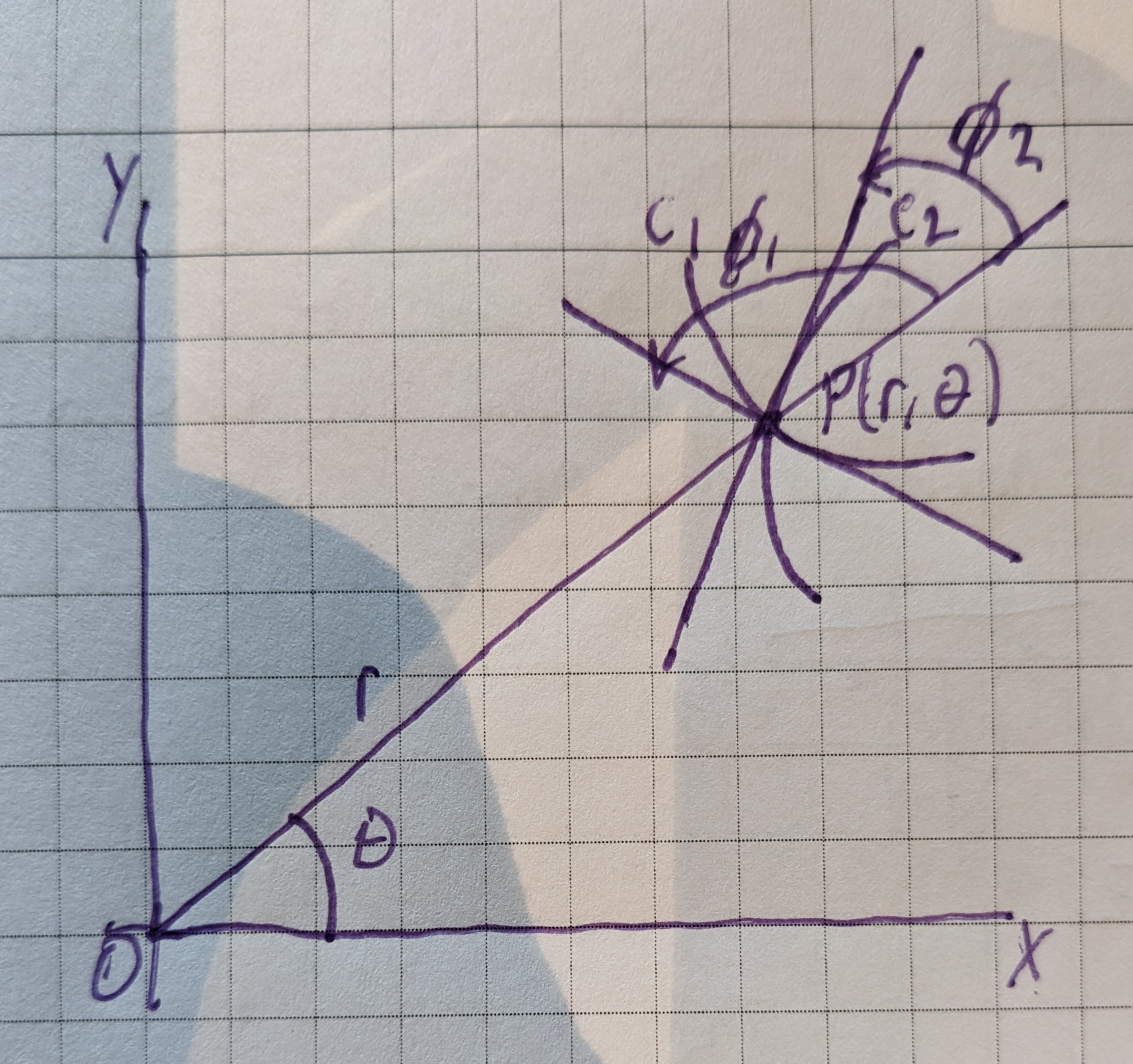
In the above figure, call $P(r,\theta)$ the point of intersection in polar coordinates of two curves $c_1,c_2$, which are orthogonal trajectories of each other. Call $\phi_1$ and $\phi_2$ the respective angle the tangent to each curve $c_1$ and $c_2$ makes with the radius vector $r$ (measured from the radius vector counterclockwise to the tangent). Since the two tangents are orthogonal, it is evient form the figure that:
$$ \phi_1 = \phi_2 + \frac{\pi}{2} $$
Therefore
$$ \tag{14.31} \tan{\phi_1} = \tan{\phi_2 + \frac{\pi}{2}} = - \frac{1}{\tan{\phi_2}} $$
As remarked previously in Example 13.3, in polar coordinates:
$$ \tag{14.32} \tan{\phi_2} = r\frac{d\theta}{dr} $$
Therefore (14.31) becomes:
$$ \tag{14.33} \tan{\phi_1} = - \frac{dr}{rd\theta} $$
Comparing (14.32) with (14.33) we see that if two curves are orthogonal, then $r\frac{d\theta}{dr}$ of one is the negative reciprocal of $r\frac{d\theta}{dr}$ of the other. Conversely, if one of two curves satisfies (14.32) and the other satisfies (14.33), then the curves are orthogonal.
Hence, to find an orthogonal family of a given family, we proceed as follows:
- Calculate $r\frac{d\theta}{dr}$ of the given family.
- Replace $r\frac{d\theta}{dr}$ by its negative reciprocal $- \frac{dr}{rd\theta}$
- The family of solutions of this new resulting differential equation is orthogonal to the given family.