lacunary - Theorem Index

Theorem Index

This page lists all mathematical theorems, lemmas, and corollaries found across the site. Click on any item to jump to its location in the notes.

Found 230 theorem/lemma/corollarys
Theorem: CN is an inner product space \@{complex-inner-product-space}

The function

⟨z,w⟩=∑k=0N−1zkwk―

defined on z,w∈CN is an inner product, and so CN (N a positive integer) forms an @inner-product-space.

Proof \@{proof-of-complex-inner-product-space}

Since C is a field, CN is obviously a vector space.

To see that this is indeed an inner product, we'll show the required properties hold.

For @conjugate-symmetry, let zk=a+bi and let wk=c+di. Then,

zkwk―=(a+bi)(c−di)=ac−adi+cbi+bd=(ac+bd)+(cb−ad)i,

and

wkzk――=(c+di)(a−bi)―=ac+adi−cbi+bd―=(ac+bd)−(ad−cb)i=(ac+bd)+(cb−ad)i,

and since k is arbitrary, it holds for any respective pair of components in z and w, and so ⟨z,w⟩=⟨w,z⟩―.

For @linearity in the first argument, let w,v,z∈Cn,a,b∈C. Then

⟨ax+by,z⟩=(ax1+by1)∗z1+(ax2+by2)∗z2+⋯=a(x1∗z1)+a(x2∗z2)+⋯+b(y1∗z1)+b(y2∗z2)+⋯=a⟨x,z⟩+b⟨x,z⟩.

Now, to show @positive-definiteness let z=a+bi. Then,

⟨z,z⟩=zz―=1>0.

◻
from Discrete Fourier Transform
Theorem: A sequence in Rk converges iff its components converge \@{sequence-in-rk-converges-iff-its-components-converge}

(a) Suppose xn∈Rk,(n=1,2,3,…) and xn=(α1,n,…,αk,n).

Then, {xn} converges to x=(α1,…,αk) if and only if

limn→∞αj,n=αj,(1≤j≤k).

(b) Suppose {xn},{yn} are sequences in Rk, {βn} is a sequence of real numbers, and xn→x,yn→y,βn→β. Then

limn→∞(xn+yn)=x+y,limn→∞xn⋅yn=x⋅y,limn→∞βnxn=βx.

Proof \@{proof-of-sequence-in-rk-converges-iff-its-components-converge}

For (a), assume xn→x. Then, from the definition of the norm,

|αj,n−αj|≤|xn−x|,

that is, the distance from αk,n to αn is always less than or equal to the distance from xn to x. Therefore, for ϵ>0, |xn−x|<ϵ⟹|αj,n−αj|<ϵ, and we can pick n to make this true for as small of ϵ as we'd like. Therefore, limn→∞αj,n=αj.

Conversely, assume limn→∞αj,n=αj. Let ϵ>0. For some integer N, when n≥N we have

|αj,n−αj|≤ϵk,(1≤j≤k).

Therefore, n≥N implies that

|xn−x|=∑j=1k|αj,n−αj|2<ϵ,

so xn→x.

Part (b) follows from part (a) and A sequence in Rk converges iff its components converge.

◻
Referenced by (2 direct)

Direct references:

from Sequences in Euclidean and Metric Spaces
Theorem: Adding an Affine Function Preserves Convexity \@{adding-an-affine-function-preserves-convexity}

Let E⊆Rk be a convex set, let φ:E→R, and let ℓ:E→R be affine. If φ is convex, then φ+ℓ and φ−ℓ are convex. If φ is concave, then φ+ℓ and φ−ℓ are concave. A linear function is affine, so this covers adding or subtracting a linear function.

TODO: prove this.

Referenced by (1 direct)

Direct references:

from Convexity
Theorem: Addition and Multiplication Rules \@{probability-rules}

The probability of A or B is the probability of A plus the probability of B minus the probability of A and B occurring together:

P(A∪B)=P(A or B)=P(A)+P(B)−P(A and B)

If A and B are mutually exclusive events, P(A∪B)=P(A)+P(B).

We have to subtract the overlap between A and B to avoid double counting.

Similarly

P(A∩B)=P(A)+P(B)−P(A∪B).

The probability of A and B is the probability of A times the probability of B given A, or equivalently, the probability of B times the probability of A given B.

P(A∩B)=P(A and B)=P(B and A)=P(A)⋅P(B|A)=P(B)⋅P(A|B)

If A and B are independent, this reduces to P(A)⋅P(B).

from Probability Basics
Theorem: Affine Precomposition Preserves Convexity \@{affine-precomposition-preserves-convexity}

Let D⊆Rk and E⊆Rm be convex sets, let A:D→E be affine, and let φ:E→R. If φ is convex, then φ∘A is convex on D. If φ is concave, then φ∘A is concave on D.

TODO: prove this.

Referenced by (1 direct)

Direct references:

from Convexity
Theorem \@{all-parameterizations-of-curve-have-same-line-integral}

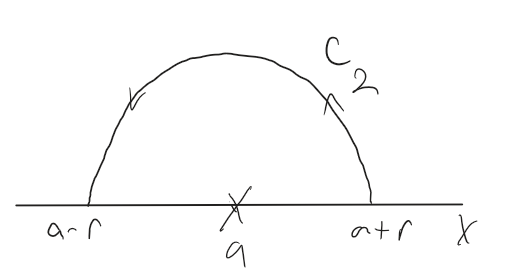
When P(x,y) and Q(x,y) are continuous and C is smooth, we can calculate the value of the line integral by expressing P,Q,dx and dy in terms of any parametric representation of C and evaluating the resulting definite integral:

∫CP(x,y)dx+Q(x,y)dy=∫αβ{P[x(t),y(t)]dxdt+Q[x(t),y(t)]dydt}dt.(4.7)

All parameterizations of the curve lead to the same value.

from Arc Length and Line Integrals
Theorem \@{analytic-implies-cr-equations}

Assume a complex function f(z) is defined on a neighborhood of z0, and f is complex differentiable at z0. Let z=x+iy and write f(x+iy)=u(x,y)+iv(x,y). Then all of the partial derivatives ux,uy,vx,vy exist and

ux=vy,uy=−vx,

and

f′(x0+iy0)=ux(x0,y0)+ivx(x0,y0).

Proof \@{proof-of-analytic-implies-cr-equations}

By assumption and definition of the complex derivative, we have that

f′(z0)=limΔz→0f(z0+Δz)−f(z0)Δz=limΔz→0[u(x0+Δx,y0+Δy)−u(x0,y0)]+i[v(x0+Δx,y0+Δy)−v(x0,y0)]Δz.

Now, this limit must exist and be the same no matter what path we take. So, we can take the path along the real axis by setting Δy=0 and sending Δx→0, and we get

f′(z0)=f′(x0+iy0)=limΔx→0[u(x0+Δx,y0)−u(x0,y0)]+i[v(x0+Δx,y0)−v(x0,y0)]Δx,

and hence,

Ref′(z0)=limΔx→0u(x0+Δx,y0)−u(x0,y0)Δx,

Imf′(z0)=limΔx→0v(x0+Δx,y0)−v(x0,y0)Δx.

This gives us that the partial derivatives ux and vx exist and

∂u∂x(x0,y0)=Ref′(x0+iy0),∂v∂x(x0,y0)=Imf′(x0+iy0),

that is,

f′(x0+iy0)=ux+ivx.(a)

Now, we can repeat this trick by sending Δz=Δx+iΔy to zero along the imaginary axis by setting Δx=0 and sending Δy→0 to get

f′(z0)=f′(x0+iy0)=limΔy→0[u(x0,y0+Δy)−u(x0,y0)]+i[v(x0,y0+Δy)−v(x0,y0)]iΔy=limΔy→0[v(x0,y0+Δy)−v(x0,y0)]−i[u(x0,y0+Δy)−u(x0,y0)]Δy,

and hence

Ref′(z0)=limΔy→0v(x0,y0+Δy)−v(x0,y0)Δy,

Imf′(z0)=−limΔy→0u(x0,y0+Δy)−u(x0,y0)Δy.

This gives us that the partial derivatives uy and vy exist and

−∂u∂y(x0,y0)=Imf′(x0+iy0),∂v∂y(x0,y0)=Ref′(x0+iy0),

that is,

f′(x0+iy0)=vy−iuy.(b)

Now, comparing (a) and (b) we have

ux+ivx=vy−iuy,ux=vy,uy=−vx.

◻
from Derivatives of Complex Functions
Theorem \@{arc-length-in-plane}

If a smooth curve x=f(t),y=g(t),a≤t≤b, is traversed exactly once as t increases from a to b, the curve's length is

L=∫abds=∫ab(dxdt)2+(dydt)2dt

The arc length of curve in R3 can be defined the same way, assuming z=h(t):

L=∫abds=∫ab(dxdt)2+(dydt)2+(dzdt)2dt

from Arc Length and Line Integrals
Theorem \@{balls-are-convex}

All balls are convex.

Proof \@{proof-of-balls-are-convex}

Let y,z be points in a ball with center x and radius r. Then, by definition, |y−x|<r, and |z−x|<r. Suppose p∈{λy+(1−λ)z|0<λ<1}. We will show that |x−p|<r.

|x−p|=|x−(λy+(1−λ)z)|(substitute definition of p)=|x−λy−z+λz|(expand)=|x−λy−z+λz+λx−λx|(add and subtract λx)=|λ(x−y)+(1−λ)(x−z)|(factor λ and 1−λ)≤λ|x−y|+(1−λ)|x−z|(triangle inequality)<λr+(1−λ)r(since |x−y|,|x−z|<r)=r(because λ+(1−λ)=1).

So, p is within our ball and therefore all balls are convex.

◻
Note \@{balls-are-convex-note}

Similar proofs can be used to show that closed balls and k-cells are also convex.

from Metric Spaces
Theorem: Basis and Dimension for Column Space \@{basis-and-dimension-for-column-space}

For an m×n matrix with r=rankA, the r @pivot columns form a @basis for the column space C(A) and dim⁡C(A)=r.

from Matrices
Theorem: Basis and Dimension for Left Nullspace \@{basis-and-dimension-for-left-nullspace}

For an m×n matrix with r=rankA, we know from Basis and Dimension for Row Space that r is the rank of A⊤, so the number of @free columns of A⊤ must be m−r and dim⁡N(A⊤)=m−r.

The left nullspace is the collection of vectors y for which A⊤y=0. Equivalently, y⊤A=0, with y and 0 row vectors - this is why we say left nullspace. To find a basis for the left nullspace we reduce an @augmented version of A:

[Am×nIm×n]→[Rm×nEm×n].

From this we get the matrix E for which EA=R, and if A is a @square, @invertible matrix, then E=A−1. The bottom m−r rows of E satisfy the equation y⊤A=0 and form a basis for the left nullspace of A.

from Matrices
Theorem: Basis and Dimension for Nullspace \@{basis-and-dimension-for-nullspace}

For an m×n matrix with r=rankA, the @special solutions to Ax=0 correspond to @free variables and form a @basis for the nullspace N(A). An m×n matrix has n−r free variables, so dim⁡N(A)=n−r.

from Matrices
Theorem: Basis and Dimension for Row Space (also defines: echelon basis) \@{basis-and-dimension-for-row-space}

For an m×n matrix with r=rankA, let R be the @reduced echelon form of A. The row space of R is the same as the row space of A - the rows of A are linear combinations of the rows of R.

The first r rows of R are the echelon basis for the row space of A and dim⁡C(A⊤)=r.

Referenced by (1 direct)

Direct references:

from Matrices
Theorem: Bayes' Theorem \@{bayes-theorem}

TODO: state and prove this.

Referenced by (2 direct)

Direct references:

from Probability Basics
Theorem \@{binary-sequences-are-uncountable}

Let A be the set of all sequences whose elements are the digits 0 and 1. This set A is uncountable.

Proof \@{proof-of-binary-sequences-are-uncountable}

Let E be a countable subset of A, and call the elements of E s1,s2,s3,…. We will construct a new sequence p in the following way:

pn=¬snn,n=1,2,3,…

That is, the nth digit of p will be the opposite of whatever the nth digit of sn is. So, p differs from s1 in the first digit, from s2 in the second digit, s3 in the third digit, and so on, so that it differs from all elements of E, and therefore is not contained in E. But, p is definitely in A since it its elements are the digits 0 and 1. Therefore, E is a proper subset of A, so any countable subset of A must be a proper subset of A. But, A can't be a proper subset of itself, and therefore A must be uncountable.

◻
Note \@{binary-sequences-are-uncountable-note}

This approach to proving this theorem is due to Cantor and is called diagonalization, and the animation below illustrates why.

Corollary \@{reals-are-uncountable}

The set of real numbers is uncountable.

Proof \@{proof-of-reals-are-uncountable}

I won't give a full proof here, but this can be accomplished by considering the binary representation of real numbers in the interval [0,1) consists of infinite sequences of 0 and 1.

◻
from Finite, Countable, and Uncountable Sets
Theorem: Binomial Series \@{binomial-series}

For complex z and complex α, we have

(1+z)α=∑n=0∞(αn)zn.

If |z|<1, the series converges absolutely for any any complex α, including negative integers.

Other convergence conditions are listed here.

Referenced by (1 direct)

Direct references:

from Taylor and Maclaurin Series
Theorem: Binomial Theorem \@{binomial-theorem}

The expansion of any nonnegative integer power n of the @binomial x+y is a sum of the form

(x+y)n=∑k=0n(nk)xn−kyk=∑k=0n(nk)xkyn−k.

Referenced by (2 direct)

Direct references:

from Binomial Theorem
Theorem: Bolzano-Weierstrass \@{bolzano-weierstrass}

Every bounded sequence in Rk contains a convergent subsequence.

Proof \@{proof-of-bolzano-weierstrass}

Note that any bounded sequence {pn}⊂Rk is a subset of some closed set, bounded and thus compact k-cell in Rk. Therefore, {pn} is a sequence in a compact metric space, and has a convergent subsequence.

◻
from Sequences in Euclidean and Metric Spaces
Theorem: Boundedness Theorem \@{boundedness-theorem}

If f is continuous on [a,b] then it's bounded on [a,b].

from Continuity
Theorem \@{cantor-bendixson-theorem}

Every closed set in a separable metric space is the union of a (possibly empty) perfect set and a set which is at most countable.

Proof \@{proof-of-cantor-bendixson-theorem}

Let X be a separable metric space and E⊂X be closed. If E is at most countable, then we are done.

Suppose that E is uncountable. Note that the proof of Suppose E⊂Rk, with E uncountable,... only uses the property that Rk is a separable metric space, and it therefore generalizes to any separable metric space. Thus E is the union of a perfect set - its condensation points, P, and a set that is at most countable, E∖P.

◻
Corollary \@{countable-closed-set-has-isolated-points}

Every countable closed set set in Rk has isolated points.

Proof \@{proof-of-countable-closed-set-has-isolated-points}

Let E be a countable closed set in Rk. Suppose for contradiction that E has no isolated points. Then every point of E is a limit point of E, and thus E is perfect set. But, every nonempty perfect set in Rk is uncountable, a contradiction. Thus, our assumption that E has no isolated points is incorrect, and E must contain isolated points.

◻
from Perfect Sets and More
Theorem \@{cantor-set-contains-no-segment}

The Cantor set contains no segment.

Proof \@{proof-of-cantor-set-contains-no-segment}

Suppose, for the sake of contradiction, that some segment (α,β)⊂P and let L=β−α. Pick some n∈N such that 1/3n<L. Now, En is the union of 2n intervals of length 1/3n, and since (α,β)⊂P, it must be the case that (α,β) is a subset of some interval of length 1/3n. However, this can't be the case, since L>1/3n, by construction. Therefore, our provision assumption is incorrect, and P contains no segment.

◻
from Cantor Set
Theorem \@{cantor-set-is-compact}

The Cantor set is compact.

Proof \@{proof-of-cantor-set-is-compact}

Clearly, P is bounded, for it lies within [0,1]. Each En is composed of the union of 2n closed intervals, and the union of finitely many closed intervals is also closed. P is then the intersection of infinitely many closed intervals, which is again closed. Therefore, P is closed and bounded, and by Heine-Borel, is compact.

◻
from Cantor Set
Theorem \@{cantor-set-is-not-empty}

The Cantor set is not empty.

Proof \@{proof-of-cantor-set-is-not-empty}

Suppose En has [α,β] as an interval and thus α,β∈En. Then, by definition, En+1 will contain [α,β−α3] and 2(β−α)3,β] as intervals, so α,β∈En+1. Note that E0 has [0,1] as an interval. By induction, all En contain 0 and 1, and therefore so does their intersection P, and P is nonempty.

◻
Referenced by (2 direct)

Direct references:

from Cantor Set
Theorem \@{cantor-set-is-perfect}

The Cantor set is a perfect set.

Proof \@{proof-of-cantor-set-is-perfect}

Let x∈P. Let r>0, and pick n∈N to be large enough that 1/3n<r. Then, x lies in one of the 2n intervals of length 1/3n in En; call it In. The endpoints of In are also in P (see The Cantor set is not empty.,) and at least one of them is not x. Since the endpoints are contained in a neighborhood of x with radius r>0, all neighborhoods of x are limit points of P, and therefore P is perfect.

◻
Corollary \@{cantor-set-is-uncountable}

Because nonempty perfect sets in Rk are uncountable, and the Cantor set is nonempty and perfect, the Cantor set is uncountable.

Referenced by (1 direct)

Direct references:

from Cantor Set
Theorem: Cauchy criterion for convergence \@{cauchy-criterion-for-convergence}

A sequence converges in Rk if and only if it is a cauchy sequence.

Proof \@{proof-of-cauchy-criterion-for-convergence}

Suppose {pn}⊂Rk converges. Then, because Rk is a metric space, {pn} is cauchy.

Conversely, suppose {pn}⊂Rk is cauchy. Then, {pn} converges.

◻
from Sequences in Euclidean and Metric Spaces
Theorem: Cauchy Integral Theorem \@{cauchy-integral-theorem}

If the derivative f′ of a complex function f is continuous in a domain containing a simple, closed, piecewise smooth curve C and its interior, then

∮cf(z)dz=0.

from Cauchy-Goursat Theorem
Theorem: Cauchy's Integral Theorem \@{cauchys-integral-theorem}

If f(z) is analytic in a @simply-connected domain D, then for every simple closed @path C in D,

∮Cf(z)dz=0.

Proof \@{proof-of-cauchys-integral-theorem}

Let f(z)=u(x,y)+i(v,y). By the definition of the contour integral, we have

∫Cf(z)dz=∫C(u+vi)(dx+dyi)=∫C(udx−vdy)+i∫C(vdx+udy).

Because f is analytic, the Cauchy-Riemann Equations tell us that u(x,y) and v(x,y) have continuous first partial derivatives, and therefore, we can apply Green's Theorem. Now, we can take the first integral and transform it

∫C(udx+(−vdy))=−∬R(vx+uy)dxdy.

But, by Cauchy-Riemann Equations, vx=−uy, so this integral evaluates to 0.

Now, for the second integral, using Green's Theorem again, we get

i∫C(vdx+udy)=i∬R(ux−vy)dxdy,

and by Cauchy-Riemann Equations, ux=vy, so this integral also evaluates to 0, which makes the overall integral 0 as well.

◻
from Cauchy-Goursat Theorem
Theorem: Cauchy-Goursat Theorem \@{cauchy-goursat-theorem}

If f is analytic inside and on a closed, piecewise smooth curve C, then

∮cf(z)dz=0.

from Cauchy-Goursat Theorem
Theorem: Cauchy-Riemann Equations \@{cauchy-riemann-equations}

A function f(z)=u(x,y)+v(x,y)i is analytic in an open set S if and only if the first partial derivatives of u(x,y) and v(x,y) are continuous on S and satisfy the Cauchy-Riemann equations therein

∂u∂x=∂v∂y,∂v∂x=−∂u∂y.(c)

In polar form, we have z=r(cos⁡θ+isin⁡θ) and set f(z)=u(r,θ)+iv(r,θ),

so the condition is then

ur=1rvθ,vr=−1ruθ.

Referenced by (1 direct)

Direct references:

from Derivatives of Complex Functions
Theorem: Cauchy-Schwarz Inequality \@{cauchy-schwarz-inequality}

For any vectors x,y∈Rn,

|⟨x,y⟩|≤‖x‖‖y‖,

where ⟨x,y⟩ denotes the @euclidean inner product and ‖x‖=⟨x,x⟩ is the @euclidean norm.

Proof \@{proof-of-cauchy-schwarz-inequality}

From Orthogonal Decomposition we have a=projba+oprojba.Taking the @euclidean norm squared of both sides gives ‖a‖2=‖projba+oprojba‖2=‖projba‖2+2⟨projba,oprojba⟩+‖oprojba‖2=‖projba‖2+‖oprojba‖2,with the middle term dropping out due to orthogonality. Now, because ‖oprojba‖2≥0,‖a‖2≥‖projba‖2.Now we'll flip sides and expand projection according to its definition‖projba‖2≤‖a‖2‖⟨a,b⟩‖b‖2b‖2≤(⟨a,b⟩‖b‖2)2‖b‖2≤⟨a,b⟩2‖b‖2≤‖a‖2⟨a,b⟩2≤‖a‖2‖b‖2.Taking the square root of both sides we get what we want to show:⟨a,b⟩2≤‖a‖2‖b‖2⟨a,b⟩≤‖a‖‖b‖.

◻
Intuition \@{cauchy-schwarz-inequality-intuition}

This is saying that the length of the projection of a onto b cannot exceed the length of a.

Referenced by (1 direct)

Direct references:

from Projection
Theorem: Central Limit Theorem \@{central-limit-theorem}

If c is a real constant and X1,X2,… are independent random variables with mean μ and standard deviation σ, then

TODO: the precise statement is cut off in the source; complete it.

Referenced by (1 direct)

Direct references:

from Limit Theorems
Theorem: Chain Rule for Entropy \@{chain-rule-for-entropy}

Let X1,X2,…,Xn be drawn according to p(x1,x2,…,xn). Then

H(X1,X2,…,Xn)=∑i=1nH(Xi|Xi−1,…,X1).

Proof \@{proof-of-chain-rule-for-entropy}

From Chain rule for joint entropy, we have

H(X1,X2)=H(X1)+H(X2|X1),H(X1,X2,X3)=H(X1)+H(X2,X3|X1)=H(X1)+H(X2|X1)+H(X3|X2,X1), ⋮H(X1,X2,…,Xn)=H(X1)+H(X2|X1)+⋯+H(Xn|Xn−1,…,X1)=∑i=1nH(Xi|Xi−1,…,X1).

◻
Referenced by (1 direct)

Direct references:

from Discrete Entropy
Theorem: Chain rule for joint entropy \@{joint-entropy-is-base-plus-conditional}

The entropy (joint entropy) of the joint event X,Y is the entropy of X plus the entropy of Y when X is known, that is,

H(X,Y)=H(X)+H(Y|X).

Proof \@{proof-of-joint-entropy-is-base-plus-conditional}

Note that

H(Y|X)=−∑x,yp(x,y)log⁡p(x,y)p(x)=−∑x,yp(x,y)log⁡p(x,y)+∑x,yp(x,y)log⁡p(x).

The first term on the RHS is just −∑x,yp(x,y)log⁡p(x,y)=H(X,Y). The second is

∑x,yp(x,y)log⁡p(x)=∑x[∑yp(x,y)]log⁡p(x)=∑xp(x)log⁡p(x)=−H(X).

Altogether, we have that H(Y|X)=H(X,Y)−H(X), or

H(X,Y)=H(X)+H(Y|X).

◻
Corollary: Chain Rule for Conditional Joint Entropy \@{chain-rule-for-conditional-joint-entropy}

H(X,Y|Z)=H(X|Z)+H(Y|X,Z).

Proof \@{proof-of-chain-rule-for-conditional-joint-entropy}

H(X,Y|Z)=∑z∈Zp(z)H(X,Y|Z=z)=∑z∈Zp(z)(H(X|Z=z)+H(Y|X,Z=z))=∑z∈Zp(z)H(X|Z=z)+∑z∈Zp(z)H(Y|X,Z=z)=H(X|Z)+H(Y|X,Z).

◻
Referenced by (2 direct)

Direct references:

Referenced by (3 direct)

Direct references:

from Discrete Entropy
Theorem: Chain Rule for Mutual Information \@{chain-rule-for-mutual-information}

I(X1,X2,…,Xn;Y)=∑i=1nI(Xi;Y|Xi−1,Xi−2,…,X1)

Proof \@{proof-of-chain-rule-for-mutual-information}

From Mutual Information and Entropy we have

I(X1,X2,…,Xn;Y)=H(X1,X2,…,Xn)−H(X1,X2,…,Xn|Y)

Then, from Chain Rule for Entropy and Chain Rule for Conditional Joint Entropy we have, simplifying,

H(X1,X2,…,Xn)−H(X1,X2,…,Xn|Y)=∑i=1nH(Xi|Xi−1,…,X1)−∑i=1nH(Xi|Xi−1,…,X1,Y)=∑i=1nH(Xi|Xi−1,…,X1)−H(Xi|Y,Xi−1,…,X1).

Now, from our definition of conditional mutual information we get

∑i=1nH(Xi|Xi−1,…,X1)−H(Xi|Y,Xi−1,…,X1)=∑i=1nI(Xi;Y|X1,X2,…,Xi−1).

◻
Referenced by (1 direct, 1 transitive)

Direct references:

Transitive (depth 1):

from Discrete Entropy
Theorem: Chain Rule for Relative Entropy \@{chain-rule-for-relative-entropy}

D(p(x,y)‖q(x,y))=D(p(x)‖q(x))+D(p(y|x)‖q(y|x)).

Proof \@{proof-of-chain-rule-for-relative-entropy}

Using relative-entropy, Multiplication Rule for Distributions, Product Rule for Logarithms, and conditional relative entropy:

D(p(x,y)‖q(x,y))=∑x∑yp(x,y)log⁡p(x,y)q(x,y)defn. of relative entropy=∑x∑yp(x,y)log⁡p(x)p(y|x)q(x)q(y|x)multiplication ruleby the product rule for logarithms:=∑x∑yp(x,y)log⁡p(x)q(x)+∑x∑yp(x,y)log⁡p(y|x)q(y|x)=D(p(x)‖q(x))+D(p(y|x)‖q(y|x))defns. of relative and conditional relative entropy

◻
from Discrete Entropy
Lemma: Change of Logarithm Base \@{change-of-logarithm-base}

Hb(X)=(logb⁡a)Ha(X).

Proof \@{proof-of-change-of-logarithm-base}

We use the Logarithm Change of Base here.

Hb(x)=−∑x∈Xp(x)logb⁡x=−(logb⁡a)∑x∈Xp(x)logb⁡xlogb⁡a=−(logb⁡a)∑x∈Xp(x)loga⁡x=(logb⁡a)Ha(X)

◻
from Discrete Entropy
Theorem: Characterization of Sufficiency \@{characterization-of-sufficiency}

Let X have probability mass function fθ(x) from the family {fθ(x)}, and let T(X) be a statistic of X. Then T(X) is a sufficient statistic for θ if and only if

I(θ;X)=I(θ;T(X))

for every probability distribution on θ.

Proof \@{proof-of-characterization-of-sufficiency}

If I(θ;X)=I(θ;T(X)), then by Data-Processing Inequality we have that θ→T(X)→X forms a Markov Chain, i.e. T(X) is a sufficient statistic for θ.

Now, assume T(X) is a sufficient statistic for θ. Then again by Data-Processing Inequality, I(θ;X)=I(θ;T(X)).

◻
Example \@{characterization-of-sufficiency-example}

For a sequence of n coin-flips with parameter θ=Pr(Xi=heads), the number of heads is a sufficient statistic for θ, because if we know the number of heads we got, knowing the specific order of heads and tails in the sequence tells us nothing more about θ, as all possible sequences with that many heads are equally likely.

from Discrete Entropy
Theorem: Chebyshev's Inequality \@{chebyshevs-inequality}

Suppose t>0 and X is a random variable with the finite mean E[X] and standard deviation σ. Then

P(|X−E[X]|≥t)≤σ2t2.

Note \@{chebyshevs-inequality-note}

Intuitively, this means that the probability that X is far away from its mean can't be too big.

Note that the upper-bound on this probability is proportional to the variance of the random variable and inversely proportional to the distance t of X from its mean. So, as the variance increases, the probability of X taking on values further from its mean also increases, and as the distance from the mean increases, the probability of X taking on values at least that far from E[X] decreases.

Also note that while Markov's Inequality only requires knowledge of the mean E[X] (the first moment), Chebyshev's Inequality requires knowledge of the variance E[X2]−E[X]2 (second moment). Also, Chebyshev's inequality works for any random variable with a variance defined, rather than just on non-negative random variables.

Proof \@{proof-of-chebyshevs-inequality}

Let X be a random variable with mean E[X] and variance σ2. Define the non-negative random variable

Y=(X−E[X])2.

By Markov's Inequality, for any a>0, we have

P(Y≥a)≤E[Y]a.

Set a=t2. Then,

P((X−E[X])2≥t2)≤E[(X−E[X])2]t2.

Since the variance of X is σ2=E[(X−E[X])2], it follows that

P((X−E[X])2≥t2)≤σ2t2.

Note that

(X−E[X])2≥t2⟺|X−E[X]|≥t.

Thus,

P(|X−E[X]|≥t)≤σ2t2.◻

◻
Referenced by (4 direct)

Direct references:

from Limit Theorems
Theorem \@{closed-orbits-impossible-in-gradient-systems}

Closed orbits are impossible in gradient systems.

Intuition \@{closed-orbits-impossible-in-gradient-systems-intuition}

If we're always moving "downhill" in some direction in a space, it's impossible to come back to where we started. This is another reason why oscillations aren't possible in one dimensional systems.

from Limit Cycles
Theorem \@{closed-path-of-path-independent-integral-is-zero}

If a line integral is independent of path in a domain D, and C is a closed, piecewise smooth curve in D that contains only points of D in its interior, its value is zero:

∮CPdx+Qdy=0

from Arc Length and Line Integrals
Theorem \@{closed-subsets-of-compact-sets-are-compact}

Closed subsets of compact sets are compact.

Proof \@{proof-of-closed-subsets-of-compact-sets-are-compact}

Suppose F⊂K⊂X, with F closed relative to X, and K compact. Let {Vα} be an open cover of F. Since Fc is open relative to X (see A set E is open iff its...), if we add it to {Vα}, we obtain an open cover of K; let's call it Ω. Since K is compact, we can obtain a finite subcover of K by discarding all but a finite number of sets from Ω; let's call it Φ. Since F⊂K, Φ is also a finite subcover of F, and therefore F is compact.

◻
Note \@{closed-subsets-of-compact-sets-are-compact-note}

If Fc∈Φ, we may, but aren't required, to exclude it, and still have a finite open cover of F.

Corollary \@{intersection-of-closed-and-compact-is-compact}

If F is closed and K is compact, then F∩K is compact.

Proof \@{proof-of-intersection-of-closed-and-compact-is-compact}

Because compact sets are closed and the intersection of two closed sets is again closed, F∩K is closed. Since F∩K⊂K and closed subsets of compact sets are compact, F∩K is compact.

◻
Referenced by (3 direct, 1 transitive)

Direct references:

Transitive (depth 1):

from Compact Sets
Theorem \@{closure-distributes-over-finite-unions}

Closure distributes over finite unions.

If Bn=⋃i=inAi, then Bn―=⋃i=1nAi―,n=1,2,3,….

Proof \@{proof-of-closure-distributes-over-finite-unions}

Let p∈⋃i=1nAi―. Then, p∈Ai― for some i. If p∈Ai, then p∈⋃i=inAi=Bn, so p∈Bn―. If p is in some Ai′, then every neighborhood of p contains some point q∈Ai,q≠p, and since Ai⊂Bn, q∈Bn, so p∈Bn―.

Conversely, let p∈Bn―. If p∈Bn, p∈Ai for some i, and thus p∈Ai―⊂⋃i=1nAi―. If p is only in Bn′, suppose for contradiction that p∉⋃i=1nAi―. For each i, let Ni be a neighborhood centered at p with Ni∩Ai=∅. Then, N=⋂i=1nNi is a neighborhood of p (see (a) - For any collection {Ga} of...,) but N∩Ni=∅ for all i, so N∩Bn=∅. But, this contradicts our hypothesis that p∈Bn―, so our contradictory assumption must be invalid, and p∈⋃i=1nAi―.

◻
from Metric Spaces
Theorem \@{compact-implies-closed}

Any compact subset K of a metric space X is closed.

Proof \@{proof-of-compact-implies-closed}

Suppose K is compact relative to metric space X. Let p∈Kc. For each q∈K, we can define rq=12d(p,q), and let Pq and Qq be neighborhoods of radius rq around p and q, respectively. Note that Pq and Qq are disjoint, because we defined their radii to be half the distance between them, and they are open.) Now, since K is compact, we can pick a finite number of points in K, q1,…,qn, such that K⊂Qq1∪⋯∪Qqn=Q (Q is a finite subcover of K.) Using the same set of points as reference, let Pq1∩⋯∩Pqn=P. Note that P∩Q={}, since each Pq is disjoint with its paired Qq (to be in P, a point must be in all Pq, but any point in Q is not in at least one Pq.) P is open, since it is the intersection of finitely many open sets (see (a) - For any collection {Ga} of...) and obviously contains p, since each Pq contains p. Therefore, p has a neigborhood P that is disjoint with K (since P∩K⊂P∩Q={}), and is therefore an interior point of Kc. It follows that Kc is open, and that K is closed.

◻
Referenced by (2 direct)

Direct references:

from Compact Sets
Theorem \@{compact-metric-space-has-countable-base}

Every compact metric space has a countable base and is therefore separable.

Proof \@{proof-of-compact-metric-space-has-countable-base}

Let K be a compact metric space. Fix n∈N (any natural number will do,) then, consider the open cover {Gα}n of balls of radius 1/n centered at x∈K. Now, because K is compact, some finite {Vα}n⊂{Gα}n covers K.

Now, consider the set of all balls for all n,

C=⋃n=1∞{Vα}n

Because the union of a sequence of countable sets is countable, C is countable. To show C is a base for K, let G be an open subset of K, and let x∈G. Let ϵ>0 such that Bϵ(x)⊂G. Pick natural n such that 1/n<ϵ/2. Then, x∈{Vα}n for some α, (because no point in K is more than 1/n away from the center of some {Vα}n and therefore C is a countable base of K. Since we can make ϵ as close to 0 as we like, the centers of {Vα}n are dense as well as countable, and are therefore a countable dense subset of K, so K is separable.

◻
from Perfect Sets and More
Theorem \@{compact-metric-spaces-are-complete}

Compact metric spaces are complete.

That is, if X is a compact metric space and if {pn} is a cauchy sequence in X, then {pn} converges to some point of X.

Proof \@{proof-of-compact-metric-spaces-are-complete}

Let {pn} be a cauchy sequence in the compact metric space X. For N=1,2,3,…, let En bet the set consisting of pN,pN+1,pN+2,…. Then

limN→∞diamEN―=0,

by two theorems above. Each En― is a closed subset of the compact space X, and is thus compact. Also, EN+1⊂EN, which implies that EN+1―⊂EN―. Now, we have that there is a unique p∈X which lies in every En―.

Let ϵ>0. Since limN→∞diamEN―=0, there is an integer N0 such that diamEn―<ϵ if N≥N0. Since p∈En―, we have that d(p,q)<ϵ for every q∈EN― and thus for every q∈En. That is, d(p,pn)<ϵ if n≥N0, so {pn} converges to p.

◻
Referenced by (1 direct)

Direct references:

Referenced by (2 direct)

Direct references:

from Sequences in Euclidean and Metric Spaces
Theorem \@{compact-relative-to-subspace}

Suppose K⊂Y⊂X. Then K is compact relative to X iff K is compact relative to Y.

Proof \@{proof-of-compact-relative-to-subspace}

Suppose K is compact relative to X and that {Vα} is an open cover of K relative to Y, such that K⊂⋃αVα. We need to show that a finite subset of {Vα} covers K. Because {Vα} is open relative to Y and Y⊂X (see Suppose Y⊂X. A subset E...) there are sets Gα, open relative to X, such that Va=Y∩Gα, for each α. Now, since K is compact relative to X, we have K⊂Gα1∪⋯∪Gαn,(a) for some finite set of indices a1,…,an. Now, since K⊂Y, K⊂Vα1∪⋯∪Vαn,(b) which shows K is compact relative to Y.

Conversely, suppose K is compact relative to Y and let {Gα} be a cover of K open relative to X. We need to show there is a finite subset of {Gα} that covers K. Let Vα=Y∩Gα, for each α. Then (b) will hold for some set of indicies, α1,…,αn, and since each Vα⊂Gα, (a) is implied by (b) and we've shown K is compact relative to X.

◻
from Compact Sets
Theorem \@{complement-of-intersection-is-union-of-complements}

The complement of an intersection is equal to the union of complements.

Proof \@{proof-of-complement-of-intersection-is-union-of-complements}

Let A and B be sets. We want to show that

(A∩B)c=Ac∪Bc.

Suppose x∈(A∩B)c. Then, x is not in A∩B, that is, x is either not in A or it is not in B or it is in neither. If x is not in A, then it is in Ac, and therefore it is in Ac∪Bc. The same approach works with B, and therefore x∈Ac∪Bc, and we have shown (A∩B)c=Ac∪Bc.

◻
from Set Theory
Theorem \@{complement-of-union-is-intersection-of-complements}

The complement of a union is equal to the intersection of complements.

Proof \@{proof-of-complement-of-union-is-intersection-of-complements}

Let A and B be sets. We want to show that

(A∪B)c=Ac∩Bc.

Suppose x∈(A∪B)c. Then, if x∈A or x∈B, then x∈A∪B and x∉(A∪B)c, a contradiction. Therefore, x∉A and x∉B. That is, x∈Ac and x∈Bc, therefore x∈Ac∩Bc.

◻
Referenced by (2 direct)

Direct references:

from Set Theory
Theorem \@{complement-of-union-is-intersection-of-complements-general}

Let Eα be a collection of sets. Then

(⋃αEα)c=⋂α(Eαc).

Proof \@{proof-of-complement-of-union-is-intersection-of-complements-general}

Suppose x∈(⋃αEα)c. Then, x∉⋃αEα, so x is not in any Eα. Therefore, for every Eα, x∈Eαc, and thus x∈⋂α(Eαc). Conversely, suppose x∈⋂α(Eαc). Then, x is in every Eαc, that is, x is not in any Eα. Therefore, x∈(⋃αEα)c.

◻
Note \@{complement-of-union-is-intersection-of-complements-general-note}

This is just De Morgan's law extended to arbitrary indexed collections.

from Metric Spaces
Theorem \@{composition-of-continuous-functions-is-continuous}

Suppose X,Y,Z are metric spaces, E⊂X, f:E→Y, g:f(E)→Z, h:E→Z with

h(x)=g(f(x))(x∈E).

If f is continuous at a point p∈E and if g is continuous at the point f(p), then h is continuous at p.

Proof \@{proof-of-composition-of-continuous-functions-is-continuous}

Let ϵ>0. Since g is continuous at f(p), there exists η>0 such that

dZ(g(y),g(f(p)))<ϵ if dY(y,f(p))<η and y∈f(E).

Since f is continuous at p, there exists δ>0 such that

dY(f(x),f(p))<η if dX(x,p)<δ and x∈E.

It follows that

dZ(h(x),h(p))=dz(g(f(x)),g(f(p)))<ϵ

if dX(x,p)<δ and x∈E. Thus, h is continuous at p.

◻
Intuition \@{composition-of-continuous-functions-is-continuous-intuition}

Basically, since g is continuous, we can control how close its output is to g(f(p)) by controlling how close its input is to f(p), which we can certainly do, since f is also continuous, and we can control how close its output is to f(p) by controlling how close its input is to p.

from Continuity in Euclidean and Metric Spaces
Theorem: Concavity and Convexity of Mutual Information \@{concavity-and-convexity-of-mutual-information}

Let (X,Y)∼p(x,y)=p(x)p(y|x). The mutual information I(X;Y) is a concave function of p(x) for fixed p(y|x) and a convex function of p(y|x) for fixed p(x).

Proof \@{proof-of-concavity-and-convexity-of-mutual-information}

For the first part, first expand mutual information:

I(X;Y)=H(Y)−H(Y|X)=H(Y)−∑xp(x)H(Y|X=x).

If p(y|x) is fixed, then

p(y)=∑xp(y|x)p(x)

is a linear function of p(x). Since H(y) is a concave function of p(y), by Affine Precomposition Preserves Convexity it is a concave function of p(x). The second term is a linear function of p(x), so by Adding an Affine Function Preserves Convexity, their difference is a concave function of p(x) as well.

For the second part, fix p(x) and consider two different conditional distributions p1(y|x) and p2(y|x). Their corresponding joint distributions are p1(x,y)=p(x)p1(y|x) and p2(x,y)=p(x)p2(y|x), and their respective marginal distributions are p(x),p1(y) and p(x),p2(y). Consider a conditional distribution formed from their convex combination

pλ(y|x)=λp1(y|x)+(1−λ)p2(y|x).

Their corresponding joint distributions are also a convex combination of the corresponding joint distributions,

pλ(x,y)=λp1(x,y)+(1−λ)p2(x,y),

and the distribution of Y is also a convex combination,

pλ(y)=λp1(y)+(1−λ)p2(y).

Now, if we let qλ(x,y)=p(x)pλ(y) be the product of the marginal distributions, we have

qλ(x,y)=λq1(x,y)+(1−λ)q2(x,y).

The mutual information is the relative-entropy between the joint distribution and the product of the marginals, so

I(X;Y)=D(pλ(x,y)‖qλ(x,y)),

and relative entropy is a convex function of (p,q), so the mutual information is a convex function of the conditional distribution.

◻
from Discrete Entropy
Theorem: Concavity of Entropy \@{concavity-of-entropy}

H(p) is a concave function of p.

Proof \@{proof-of-concavity-of-entropy}

Let u be the uniform distribution on |X| outcomes. Then from the definition of @relative-entropy,

D(P‖u)=H(p,u)−H(p)⟺H(p)=H(p,u)−D(p‖u).

Then, from the definition of cross-entropy

H(p,u)=−∑x∈Xp(x)log⁡u(x)=−∑x∈Xp(x)log⁡1|X|=−∑x∈Xp(x)(log⁡1−log⁡|X|)=∑x∈Xp(x)log⁡|X|=log⁡|X|

So,

H(p)=log⁡|X|−D(p‖u),

and by Convexity of Relative Entropy, entropy is a concave function.

◻
Intuition \@{concavity-of-entropy-intuition}

The intuition is that mixing distributions can never decrease uncertaintity.

Convexity of Relative Entropy The image above was generated using GPT-5.6 Sol.

We already proved Uniform distribution maximizes entropy using Lagrangian multipliers, but the proof above shows it in another way. If p=u, then D(p‖u)=0, and since log⁡|X| is constant in |X|, H is maximized by u.

from Discrete Entropy
Theorem \@{condensation-points-of-an-uncountable-subset-of-rk-are-perfect}

Suppose E⊂Rk, with E uncountable, and let P be the set of all condensation points of E. Prove that P is perfect and that at most countably many points of E are not in P, that is, that Pc∩E is at most countable.

Proof \@{proof-of-condensation-points-of-an-uncountable-subset-of-rk-are-perfect}

Let {Vn} be a countable base of Rk (see Rk is separable. and Every separable metric space has a countable...,) and let W be the union of those Vn for which E∩Vn is at most countable. We will show that P=Wc.

Suppose p∈Wc. Then p is in no Vn for which Vn∩E is at most countable, that is, every neighborhood of p has uncountably many points in E, and thus p∈P.

Conversely, suppose p∈P. Suppose, for the sake of contradiction, that p∈W. Then p∈Vn for some Vn where Vn∩E is at most countable. But, since p is an interior point of this Vn, there is a neighborhood N(p)⊂Vn, and since every neighborhood of p has uncountably many points in E, we have a contradiction, and thus our assumption that p∈W must be incorrect, and therefore p∈Wc, and P=Wc. Furthermore, since W is a union of open sets, W is open, and Wc=P is closed.

Since W is open, only countably many Vn are required to cover it. Each of these Vn has at most countably many points in E, so W=Pc has at most countably many points in E, that is, there are at most countably many points of E that are not in P.

Now, to show all points in P are limit points of P, suppose p∈P. Let Nr(p),r>0 be a neighborhood of p. Then, Nr(p)∩E is uncountable. Now, since there are at must countably many points in E that are not in P, there are at most countably many points in (Nr(p)∩E)∖P, and therefore there must be uncountably many points in Nr(p)∩E∩P. Therefore, every neighborhood of p contains infinitely many points in P other than p, p is a limit point of P, and P is perfect.

◻
Referenced by (1 direct)

Direct references:

from Perfect Sets and More
Theorem: Conditional Independence Given Intermediate Step \@{conditional-independence-given-intermediate-step}

Random Variables X,Y,Z form a markov chain X→Y→Z if and only if X and Z are conditionally independent given Y.

Proof \@{proof-of-conditional-independence-given-intermediate-step}

Suppose X and Z are conditionally independent given Y. Then, using Bayes' Theorem we have

p(x,z|y)=p(x|y)p(z|y)=p(x)p(y|x)p(z|y)p(y)

Then,

p(x,y,z)=p(y)p(x|y)p(z|y)=p(y)p(x)p(y|x)p(z|y)p(y)=p(x)p(y|x)p(z|y).

Now assume we have Markovicity, i.e p(x,y,z)=p(x)p(y|x)p(z|y). Again, using Bayes:

p(x,y,z)=p(x)p(y|x)p(z|y)=p(x)p(x|y)p(y)p(z|y)p(x)=p(x|y)p(y)p(z|y).

So, for a fixed y we have p(x,y,z)p(y)=p(x|y)p(z|y).

◻
from Markov Chains
Theorem: Conditioning Reduces Entropy \@{conditioning-reduces-entropy}

The uncertainty of Y is never increased by knowledge of X. It will be decreased unless X and Y are independent events, in which case it is not changed.

Proof \@{proof-of-conditioning-reduces-entropy}

From Let X and Y be discrete random... and Chain rule for joint entropy, we have

H(X)+H(Y)≥H(X,Y)=H(X)+H(Y|X),

hence H(Y)≥H(Y|X).

◻
Referenced by (1 direct)

Direct references:

from Discrete Entropy
Theorem: Confidence Interval for a Mean, Known Variance \@{ci-mean-known-variance}

If x¯ is the mean of a random sample of size n from a population with a known variance σ2, a 100(1−α)% confidence interval for μ is given by

x¯−zα/2σn<μ<x¯+zα/2σn.

from Confidence Intervals
Theorem: Confidence Interval for a Mean, Unknown Variance \@{ci-mean-unknown-variance}

If x¯ is the mean of a random sample of size n from a population with an unknown variance, and the standard deviation of the sample is s, a 100(1−α)% confidence interval for μ is given by

x¯−tα/2sn<μ<x¯+tα/2sn.

from Confidence Intervals
Theorem \@{connected-sets-in-r1-are-intervals}

A subset E of the real line R1 is connected if and only if it has the following property: If x∈E,y∈E, and x<z<y, then z∈E.

Proof \@{proof-of-connected-sets-in-r1-are-intervals}

We will proceed both sides of the implication by proving the contrapositive, i.e., that if the interval property doesn't hold, then the set isn't connected, and conversely, that if the set isn't connected, the interval property doesn't hold.

Suppose x,y∈E and z∈(x,y),z∉E. Then E=Az∪Bz, where

Az=E∩(−∞,z),Bz=E∩(z,∞).

Since x∈Az and y∈Bz, they are nonempty, and since Az⊂(−∞,z) and Bz⊂(z,∞), they are separated. Therefore, E is not connected.

Conversely, suppose, for the sake of contradiction, that E is not connected. Then there are nonempty separated sets A an B such that A∪B=E. Let x∈A,y∈B and assume x<y. Define

z=sup(A∩[x,y]).

By Let E be a nonempty set of..., z∈A―, and because A and B are separated, z∉B. Therefore x≤z<y.

If z∉A, it follows that x<z<y, and z∉E.

If z∈A, then z∉B―, hence there exists z1 such that z<z1<y and z1∉B (because z∉B― means there is a neighborhood of z that contains no points of B.) Thus, x<z1<y and z1∉E.

◻
from Connected Sets
Theorem: Conservative Sample Size for Estimating a Proportion \@{sample-size-proportion-conservative}

If p^ is used as an estimate of p, we can be at least 100(1−α)% confident that the error will not exceed a specified amount e when the sample size is

TODO: the sample-size formula is missing from the source; complete this statement.

from Confidence Intervals
Theorem \@{conservative-systems-have-no-attracting-fixed-points}

Conservative systems have no attracting fixed points.

Proof \@{proof-of-conservative-systems-have-no-attracting-fixed-points}

Suppose x∗ were an attracting fixed point in a conservative system. Then, note that all trajectories in the basin of attraction approach x∗ as t→∞. Since E(x) is continuous, the energy in the limit as trajectories approach x∗ is equal to the energy at the fixed point, and so the energy along the entirety of each trajectory is equal to the energy at the fixed point. But, this implies that the energy in the entire basin of attraction is the same as the energy at the fixed point, which violates our definition of a conservative system (i.e. we require that E(x) be nonconstant.) Therefore no such fixed point can exist.

◻
from Limit Cycles
Theorem: Continuity Theorem for Moment Generating Functions \@{mgf-continuity-theorem}

Let {Xn} be a sequence of random variables with moment generating functions defined by

MXn(t)=E[etXn]

for all |t|<ϵ for some ϵ>0.

Suppose there exists a function M(t), finite for |t|<ϵ, such that

limn→∞MXn(t)=M(t)

for all |t|<ϵ, and that M(t) is the moment generating function of some random variable X.

Then the distributions of {Xn} converge in distribution to X, i.e.,

Xn→dX.

from Limit Theorems
Theorem \@{convergent-sequences-are-bounded}

If {pn} converges, then {pn} is bounded (sequence).

Proof \@{proof-of-convergent-sequences-are-bounded}

Let ϵ>0. Only finitely many points in {pn} lie outside of Bϵ(p). That is, for some integer N, only the points pn where n≤N lie outside of Bϵ(p). Let δ=max{ϵ,d(p,p1),d(p,p2),…,d(p,pn)},n=1,2,…,N. Then, d(p,pn)<δ for all n=1,2,3,….

◻
from Sequences in Euclidean and Metric Spaces
Theorem: Convexity of Relative Entropy \@{convexity-of-relative-entropy}

D(p‖q) is convex in the pair (p,q); that is, if (p1,q1) and (p2,q2) are two pairs of probability mass functions, then

D(λp1+(1−λ)p2‖λq1+(1−λ)q2)≤λD(p1‖q1)+(1−λ)D(p2‖q2)

for all 0≤λ≤1.

Proof \@{proof-of-convexity-of-relative-entropy}

First, note that the set of probability mass functions on X is the set of probability vectors in Rn, where n=|X|, and thus is a convex set. D takes a pair (p,q)∈Rn×Rn, which is again convex, so D is defined on a convex set.

Now we'll apply Log Sum Inequality to the one term with a fixed x left-hand side of the inequality in the theorem, but we'll do some replacements to make it more obvious what's happening.

Let a1=λp1(x),a2=(1−λ)p2(x)b1=λq1(x),b2=(1−λ)q2(x).

Using those substitutions, with Log Sum Inequality, we have

(λp1(x)+(1−λ)p2(x))log⁡λp1(x)+(1−λ)p2(x)λq1(x)+(1−λ)q2(x)=(a1+a2)log⁡a1+a2b1+b2≤a1log⁡a1b1+a2log⁡a2b2=λp1(x)log⁡λp1(x)λq1(x)+(1−λ)p2(x)log⁡(1−λ)p2(x)(1−λ)q2(x)=λp1(x)log⁡p1(x)q1(x)+(1−λ)p2(x)log⁡p2(x)q2(x)

Summing both sides of this over x∈X gives us

D(λp1+(1−λ)p2‖λq1+(1−λ)q2)≤λD(p1‖q1)+(1−λ)D(p2‖q2).

◻
Intuition \@{convexity-of-relative-entropy-intuition}

relative-entropy is a convex @surface over @pairs (p,q), with a flat-bottomed zero valley along p=q, rising as p and q differ.

Convexity of Relative Entropy The image above was generated using GPT-5.6 Sol.

Another way to think of this is that mixing p1 and p2, and q1 and q2 can't make the results more distinguishable than the weighted average distinguishabilities between p1 and q1 and p2 and q2, i.e., mixing distributions tends to wash out distinctions.

Referenced by (1 direct)

Direct references:

from Discrete Entropy
Theorem \@{cos-characterization-of-dot-product}

The dot product of u and v is

u⋅v=|u||v|cos⁡θ

where θ is the angle between u and v.

Referenced by (1 direct)

Direct references:

from Properties of Vectors
Theorem: Countable Sets Have Outer Measure 0 \@{countable-sets-have-outer-measure-0}

Every countable subset of R has outer measure 0.

Corollary \@{corollary-4}

From this and The set of rational numbers is countable., we have that |Q|=0.

from Outer Measure
Theorem: Countable subadditivity of outer measure \@{countable-subadditivity-of-outer-measure}

Suppose A1,A2,… is a sequence of subsets of R. Then

|⋃k=1∞Ak|≤∑k=1∞|Ak|.

from Outer Measure
Theorem \@{cyclic-subgroup-generated-by-powers}

Let G=⟨a⟩ be a cyclic group with n elements. Let b∈G and b=as. Then b generates a cyclic subgroup of G containing nd elements, where d=gcd(s,n). Two cyclic subgroups ⟨as⟩ and ⟨at⟩ are equal if and only if gcd(s,n)=gcd(t,n).

Proof \@{proof-of-cyclic-subgroup-generated-by-powers}

Suppose g∈G with ord(g)=n and let m∈N. Then, ⟨gm⟩=⟨ggcd(m,n)⟩.

So, ⟨g⟩=⟨gm⟩⟺gcd(m,n)=1.

◻
from Groups
Theorem: Data-Processing Inequality \@{data-processing-inequality}

If X→Y→Z, then I(X;Y)≥I(X;Z).

Proof \@{proof-of-data-processing-inequality}

Using Chain Rule for Mutual Information, we can expand I(X;Y,Z) in two ways:

I(X;Y,Z)=I(X;Z)+I(X;Y|Z)=I(X;Y)+I(X;Z|Y).

Now, X and Z are conditionally independent given Y, so I(X;Z|Y)=0, and recalling that I(X;Y|Z)≥0 we have

I(X;Y)=I(X;Z)+I(X;Y|Z)⟺I(X;Y)≥I(X;Z).

We have equality if and only if I(X;Y|Z)=0, i.e. if X→Z→Y forms a markov chain.

◻
Referenced by (1 direct)

Direct references:

Corollary: Processing Cannot Increase Information \@{processing-cannot-increase-information}

If Z=g(Y), we have I(X;Y)≥I(X;g(Y)).

Proof \@{proof-of-processing-cannot-increase-information}

From Function of middle variable forms Markov Chain we have that X→Y→g(Y) is a markov chain and Data-Processing Inequality gives us I(X;Y)≥I(X;g(Y)).

◻
Corollary \@{corollary-77}

If X→Y→Z, then I(X;Y|Z)≤I(X;Y).

Proof \@{proof-of-corollary-77}

In Using Chain Rule for Mutual Information, we... we showed that I(X;Z|Y)=0 and I(X;Z)≥0. Then,

I(X;Z)+I(X;Y|Z)=I(X;Y)⟺I(X;Y|Z)≤I(X;Y).

◻
Referenced by (4 direct)

Direct references:

from Discrete Entropy
Theorem: de Moivre's Theorem \@{de-moivres-}

zn=rn(cos⁡nθ+isin⁡nθ)

from Algebraic Properties
Theorem \@{diameter-of-set-equals-diameter-of-closure}

If E― is the closure of a set E in a metric space X, then

diamE―=diamE.

Proof \@{proof-of-diameter-of-set-equals-diameter-of-closure}

Because E⊂E―, diamE≤diamE―.

Conversely, Let p,q∈E―, and p′,q′∈E, such that d(p,p′)<ϵ,d(q,q′)<ϵ. Therefore, by the triangle inequality,

d(p,q)≤d(p,p′)+d(p′,q′)+d(q′,q)<2ϵ+d(p′,q′)≤2ϵ+diamE.

Therefore, diamE―≤2ϵ+diamE, and since ϵ was arbitrary, diamE―=diamE.

◻
Referenced by (1 direct, 1 transitive)

Direct references:

Transitive (depth 1):

from Sequences in Euclidean and Metric Spaces
Theorem \@{directional-derivative-is-inner-product-of-vector-and-grad}

The directional derivative of f in the direction of a unit vector u is the inner product of u and gradf, that is,

Du=u⋅gradf.

Referenced by (1 direct)

Direct references:

from Vector Differential Calculus
Theorem: Divergence Theorem of Gauss \@{divergence-theorem}

Let T be a closed bounded region in a space whose boundary is a @piecewise smooth @orientable surface S. Let F(x,y,z) be a vector function that is continuous and has continuous first partial derivatives in some domain containing T. Then

∭TdivFdV=∬SF⋅ndA.

from Vector Integral Calculus
Theorem: Divergence Theorem, or, Gauss's Theorem \@{divergence-theorem-or-gausss-theorem}

An important theorem related to divergence is the Divergence Theorem (also known as Gauss's theorem) which connects the flux of a vector field through a closed surface to the divergence of the field inside the volume bounded by the surface:

∭V(∇⋅F)dV=∮sF⋅dS

from Vector Differential Calculus
Theorem: Doubly stochastic maps increase entropy \@{doubly-stochastic-maps-increase-entropy}

Take a @doubly-stochastic matrix A and probability vector p, let q=Ap. Then H(q)≥H(p), with equality iff q is a @rearrangement of p.

Proof \@{proof-of-doubly-stochastic-maps-increase-entropy}

Note that qi=∑jAijpj, by the definition of vector matrix multiplication. Now we'll define a couple of joint distributions:

rij=Aijpj,sij=Aijqi.

Now we find the relative-entropy from s to r:

D(r‖s)=∑i,jrijlog⁡rijsij=∑i,jAijpjlog⁡AijpjAijqi=∑i,jAijpjlog⁡pjqi=∑i,jAijpj(log⁡pj−log⁡qi)=∑i,jAijpjlog⁡pj−∑i,jAijpjlog⁡qi

Now, addressing the first term on the RHS of the last line:

∑i,jAijpjlog⁡pj=∑j[pjlog⁡pj∑iAij]=∑j[pjlog⁡pj⋅1]=∑jpjlog⁡pj=−H(p).

And the second term on the RHS of the last line:

∑i,jAijpjlog⁡qi=∑i[log⁡qi∑jAijpj]=∑i[log⁡qiqi]=−H(q).

So, we end up with D(r‖s)=H(q)−H(p). Since D(r‖s)≥0 by Gibbs' Inequality, we have H(q)−H(p)≥0, which implies that H(q)≥H(p), which is what we wanted to show.

Now, the equivalence case. If q is just a rearrangement of p, then obviously it has the same entropy as we can just re-index to recover p. Now assume H(p)=H(q). Then, H(q)−H(p)=0⟹D(r‖s)=0⟹r=s⟹Aijpj=Aijqi⟹pj=qi whenever Aij>0. Now, for each value c appearing in p or q, let

Jc={j:pj=c},Ic={i:qi=c},

that is Jc is the set of indices of p where pj=c, and similarly with Ic and q. Now, consider row i∈Ic. For any Aij>0, we have pj=qi, so j∈Jc, i.e. every nonzero entry of row i lies in a column of Jc, so the columns j∈Jc have the entire mass of row i. Similarly, for column j∈Jc, for nonzero Aij, qi=pj=c, so i∈Ic, and the rows Ic contain all of column j's mass. Taking 1S as the @indicator-vector of a set S, we have that

A1Jc=1Ic,

that is, rows in Ic sum to 1 over the columns Jc, while rows outside Ic have no mass in the columns Jc at all. Now we count the mass:

|Ic|=1⊤1Iccount entries via dot product=1⊤(A1Jc)identity from above=(1⊤A)1Jcassociativity=1⊤1Jccolumn-stochasticity=|Jc|count entries via dot product.

Therefore, |Ic|=|Jc| for all c, so each c appears equally often in p and in q, and q is therefore a rearrangement of p.

◻
Intuition \@{doubly-stochastic-maps-increase-entropy-intuition}

Averaging (well, replacing each probability with a convex combination of all the probabilities in a way that retains their summing to 1) the probabilities in p can only bring them closer to each other (if it doesn't just rearrange them), which increases entropy.

from Discrete Entropy
Theorem \@{euclidean-space-is-metric-space}

(Rn,d:Rn→R=|x−y|) is a metric space for any n≥0.

Proof \@{proof-of-euclidean-space-is-metric-space}

First, for n=0, R0 is just the empty set, so the metric axioms are vacuously satisfied for all points in the set. Now, for n≥1,

  • Let p,q∈Rn,p≠q. Then |p−q|<0, so d(p,q)>0.
  • Let p∈Rn. Now, p−p=0, so |p−p|=0, so d(p,p)=0.
  • Let p,q∈Rn. |p−q|=|q−p|, so d(p,q)=d(q,p).
  • Let p,q,r∈Rn. |p−q|≤|p−r|+|r−p|, so d(p,q)≤d(p,r)+d(r,p).

Therefore, d is a metric on Rn and (Rn,d) is a metric space.

◻
from Metric Spaces
Theorem \@{euclidean-space-is-separable}

Rk is separable.

Proof \@{proof-of-euclidean-space-is-separable}

The points of Rk that have only rational coordinates are a subset of Rk, we'll call it Qk, countable and dense.

We know that the rationals are countable, and because n-tuples of countable elements are countable, Qk is countable.

To show Qk is dense, consider an arbitrary point p in Rk. Now, let ϵ>0. Since the the rationals are dense in the reals, we can pick a q∈Qk with d(p,q)<ϵ, by picking rational approximations of the coordinates of p and forming q such that q is within ϵ of p, i.e.

|pi−qi|<ϵk⟹|p−q|<∑i=1k(pi−qi)2<k⋅ϵk=ϵ.

◻
Referenced by (1 direct)

Direct references:

from Perfect Sets and More
Theorem \@{euclidean-spaces-are-complete}

All Euclidean spaces are complete

That is, in Rk, every cauchy sequence converges.

Proof \@{proof-of-euclidean-spaces-are-complete}

Let {xn} be a cauchy sequence in Rk. Define EN as in the proof above, but with xi in place of pi. For some N,diamEn<1. The range (sequence) of {xn} is the union of En and the finite set {x1,…,xN−1}. Hence, {xn} is bounded (sequence) (since the finite set of points can be contained in some bounding box, and the remaining points can be contained in some ball with diameter 1.) Since {xn}― is bounded, it is compact, and thus {xn} is a subset of a compact metric space (its closure), and so converges.

◻
Referenced by (1 direct)

Direct references:

from Sequences in Euclidean and Metric Spaces
Theorem \@{every-convergent-sequence-in-a-metric-space-is-a-cauchy-sequence}

Every convergent sequence in a metric space X is a Cauchy sequence.

Proof \@{proof-of-every-convergent-sequence-in-a-metric-space-is-a-cauchy-sequence}

Suppose {pn} is a convergent sequence in a metric space X. Let ϵ>0. Then for some N,d(p,pn)<ϵ when n≥N. Thus,

d(pn,pm)≤d(p,pn)+d(p,pm)<2ϵ

whenever n,m≥N, and so {pn} is Cauchy.

◻
Referenced by (1 direct)

Direct references:

from Sequences in Euclidean and Metric Spaces
Theorem \@{every-k-cell-is-compact}

Every k-cell is compact.

Proof \@{proof-of-every-k-cell-is-compact}

Let I be a k-cell, consisting of all points x=(x1,…,xk) such that aj≤xj≤bj,1≤j≤k. Let δ=∑j=1k(bj−aj)2, i.e., the maximum distance between any two points in I (the diagonal). Then for any points x,y∈I,|x−y|≤δ.

Suppose, for the sake of contradiction, that there is an open cover {Gα} of I that contains no finite subcover of I. Now, let cj=(aj+bj)/2, i.e. cj is the midpoint of [aj,bj]. We can subdivide I into 2k k-cells Qi, determined by the intervals [aj,cj] and [cj,bj]. At least one Qi, call it I1, cannot be covered by any finite subcollection of {Gα}, or else I would have a finite subcover in {Gα}. We then can subdivide I1 and so on, obtaining a sequence {In} with the following properties:

(a) In+1⊂In (each k-cell in the sequence is nested in the previous.)

(b) In is not covered by any finite subset of {Gα}.

(c) If x,y∈In, then |x−y|≤2−nδ.

From (a) and If In is a sequence of intervals..., there is some point x∗ that is in every In. For some α,x∗∈Gα, since {Gα} is a cover of all of I. Gα is open, so for some r>0,|y−x∗|<r implies that y∈Gα, that is, x has a neighborhood that lies entirely within Gα. If we make n big enough, we have that 2−nδ<r, so by (c), In⊂Gα, that is, In is entirely covered by Gα. But, this contradicts (b), so our provisional assumption is incorrect, and {Gα} must have a finite subcover that covers I, and therefore I is compact.

◻
Intuition \@{every-k-cell-is-compact-intuition}

If a k-cell has an open cover {Gα}, then any point in it will be in some Gα, and can therefore be surrounded by an open ball with some positive radius, lying entirely in Gα. That open ball takes up some space, and we can then subdivide the k-cell into small enough parts that some part is entirely within that open ball. We still have finitely many subdivisions, and each of those could be covered with a similary constructed open ball, which means we can cover the entire k-cell with finitely many open balls covered by finitely many elements of {Gα}.

Referenced by (2 direct)

Direct references:

from Compact Sets
Theorem \@{every-metric-space-where-every-infinite-subset-has-a-limit-point-is-separable}

Let X be a metric space in which every infinite subset has a limit point. Then X is separable.

Proof \@{proof-of-every-metric-space-where-every-infinite-subset-has-a-limit-point-is-separable}

Let δ>0, and pick x1∈X. Now, continue picking xj+1 such that d(xi,xj+1)≥δ i.e. so that each new point is at least δ away from each existing point. Suppose this process continues infinitely; then the points {xi} are an infinite subset of X, and thus must have a limit point p. Now, because every neighborhood of p must contain infinitely many points in xi, we can let r=δ/2, Nrp be a neighborhood of p, and pick x,y∈{xi},Nrp. But, by the triangle inequality

d(x,y)≤d(x,p)+d(p,y)<δ/2+δ/2=δ

so d(x,y)<ϵ, which contradicts our assumption that {xi} could be an infinite set where all points were at least δ apart. Therefore, {xi} has only finitely many points, and X can be covered with finitely many open balls of radius δ (for if it couldn't be, we could always fit another point into {xi}.)

Now, if we let δ=1/n,n=1,2,3,…, we can consider the set of points {xi}n as the finite set of points at least 1/n apart in X. The collection of all such points can be called {xin} and is dense in X: let p be a point in X. and Nrp,r>0 a neighborhood of p. If we pick n such that 1/n<r, then some {xi}n will be in Nrp, because if not, we would have a contradiction with the fact that shown above that no point in X is more than 1/n away from a point in {xi}n.

Since each {xi}n is finite, and there are countably many {xi}n, the {xin} is a countably dense subset of X and therefore X is separable.

◻
Referenced by (1 direct)

Direct references:

from Perfect Sets and More
Theorem \@{every-neighborhood-is-an-open-set}

Every neighborhood is an open set.

Proof \@{proof-of-every-neighborhood-is-an-open-set}

Suppose Nr(p) is a neighborhood in X. Let q∈Nr(p). We need to show that q is an interior point of Nr(p). Let s=r−d(p,q); because d(p,q)<r, we have s>0. Now let Ns(q) be the neighborhood of radius s around q. We need to show that Ns(q)⊂Nr(p). Suppose x∈Ns(q). First note that because s=r−d(p,q), d(p,q)=r−s. Now,

d(p,x)≤d(p,q)+d(q,x)<r−s+s=r.

Therefore, Ns(q)⊂Nr(p), so q is an interior point of Nr(p), and since q was arbitrary, every point of Nr(p) is interior. Hence, Nr(p) is open.

◻
Referenced by (1 direct)

Direct references:

from Metric Spaces
Theorem \@{every-separable-metric-space-has-a-countable-base}

Every separable metric space has a countable base.

Proof \@{proof-of-every-separable-metric-space-has-a-countable-base}

Let X be a separable metric space, and let x∈G⊂X, with G @open-set. Now, because X is separable, it by definition has a countable dense subset E. If x∈E, we can pick a rational δ>0 and let Nδ(x) be a neighborhood such that Nδ(x)⊂G (δ must also be small enough such that this neighborhood is within G, which is possible because x is an interior point of G and we can pick a rational as close to any real as we'd like.) Now we have that x∈Nδ(x)⊂G, and since there are countably many x∈E and countably many neighborhoods with rational radius around each x∈E, there are countably many such neighborhoods in G. On the other hand, if x∉E, then x is a limit point of E, and thus there is p∈E as close as we'd like to x. Pick p∈E such that d(p,x)<δ for some rational δ such that x⊂Nδ(p)⊂G. Again, since there are countably many such p∈E, with countably many neighborhoods of rational radius each, there are countably many such neighborhoods in G.

Now, if we let G be the union of all open sets Gβ⊂X, then G is open, and let Vα be the union of all the Nr(q),q∈G∩E, with r∈Q, then every x∈G is in some Vα, and there are countably many Vα, so Vα is a countable base for X.

◻
Referenced by (2 direct)

Direct references:

from Perfect Sets and More
Theorem \@{existence-and-uniqueness-of-ivp-solutions}

Consider the @initial-value-problem

x˙=f(x),x(0)=x0.

Suppose that f(x) and f′(x) are continuous on an open interval R of the x-axis, and suppose that x0 is a point in R. Then, the initial value problem has a solution x(t) on some time interval (−τ,τ) about t=0, and the solution is unique.

from Flows on the Line
Theorem: Extreme Value Theorem \@{extreme-value-theorem}

If f is continuous on [a,b] then f attains absolute minimum and absolute maximum values on [a,b].

Referenced by (2 direct)

Direct references:

from Continuity
Theorem: Fano's Inequality \@{fanos-inequality}

For any estimator X^ such that X→Y→X^, with Pe=Pr(X≠X^), we have

H(Pe)+Pelog⁡|X|≥H(X|X^)≥H(X|Y).

Remark \@{fanos-inequality-remark}

We're treating Pe as a parameter in a @Bernoulli distribution with probabilities

(Pe,1−Pe).

So, H(Pe) is the entropy of that distribution, i.e.

H(Pe)=−(Pelog⁡Pe+(1−Pe)log⁡(1−Pe)).

Now, if X^=g(Y), and Pe=Pr(X^≠X)=0, then if we know Y, we know X, so it follows that Pe=0 implies H(X|Y)=0.

Proof \@{proof-of-fanos-inequality}

First, we'll ignore the effect of Y and prove the first inequality

H(Pe)+Pelog⁡|X|≥H(X|X^).

Let's define a random variable E as

E={1X^≠X0X^=X.

Now we'll use Chain Rule for Conditional Joint Entropy to expand H(E,X|X^) in two ways:

H(E,X|X^)=H(X|X^)+H(E|X,X^)=H(E|X^)+H(X|E,X^)

A few things to note:

  • Because H(E)=−(Pelog⁡Pe+(1−Pe)log⁡(1−Pe)), we have that H(E)=H(Pe).
  • Since E is a function of X and X^, H(E|X,X^)=0.
  • Because Conditioning Reduces Entropy, H(E|X^)≤H(E)=H(Pe).

We can bound the remaining term as follows:

H(X|E,X^)=Pr(E=0)H(X|X^,E=0)+Pr(E=1)H(X,X^,E=1)≤(1−Pe)0+Pelog⁡|X|,

because E=0⟹X=X^⟹H(X|X^)=0, and given E=1, we can upper bound the conditional entropy as H(X)≤log⁡|X|.

Now, taking

H(E|X^)+H(X|E,X^)=H(X|X^)

and replacing the terms on the left with the upper bounds for them we found, we have

H(Pe)+Pelog⁡|X|≥H(X|X^).

Now, by the Data-Processing Inequality, we have I(X;X^)≤I(X;Y) because X→Y→X^ is a markov chain, and therefore H(X|X^)≥H(X|Y), and finally

H(Pe)+Pelog⁡|X|≥H(X|X^)≥H(X|Y).

◻
Corollary: Weak Form of Fano's Inequality \@{weak-form-of-fanos-inequality}

Under the hypotheses of Fano's Inequality,

1+Pelog⁡|X|≥H(X|Y)

or

Pe≥H(X|Y)−1log⁡|X|.

Proof \@{proof-of-weak-form-of-fanos-inequality}

This follows because H(Pe)≤1.

◻
Corollary \@{corollary-88}

Take X^=Y in Fano's Inequality. For any two random variables X and Y, let p=Pr(X≠Y). Then

H(p)+plog⁡|X|≥H(X|Y).

Proof \@{proof-of-corollary-88}

Let X^=Y in Fano's Inequality.

◻
Corollary \@{corollary-90}

Let Pe=Pr(X≠X^), and let X^:Y→X; then

H(Pe)+Pelog⁡(|X|−1)≥H(X|Y).

Proof \@{proof-of-corollary-90}

If the estimator g(Y) takes values in the set X, then the number of possible values of X when X≠Y is reduced by 1, so we can strengthen the inequality from Fano's Inequality to

H(Pe)+Pelog⁡(|X|−1)≥H(X|Y).

◻
Remark \@{fanos-inequality-remark-2}

With no knowledge of Y, let X∈{1,…,m} with p1≥p2≥⋯≥pm. The best guess is X^=1, so Pe=1−p1, and the previous corollary becomes

H(Pe)+Pelog⁡(m−1)≥H(X).

The distribution (1−Pe,Pem−1,…,Pem−1) achieves equality.

Thus, Fano's Inequality is @sharp, i.e., its bound cannot be improved.

Referenced by (5 direct)

Direct references:

from Discrete Entropy
Theorem \@{find-tangent-plane}

If S is given by F(x,y,z)=0, then at P=(x0,y0,z0), the tangent plane is

∇F(P)⋅⟨x−x0,y−y0,z−z0⟩=0.

from Vector Differential Calculus
Theorem: Finite Geometric Series \@{finite-geometric-series}

Let w∈C and N be a positive integer. Then

∑k=0N−1wk=1−wN1−w.

Proof \@{proof-of-finite-geometric-series}

First, define SN as

SN=∑k=0N−1wk=1+w+w2+⋯+wN−1.

Then

SN=1+w+w2+⋯+wN−1wSN=w+w2+w3+⋯+wN

Subtracting the second equation from the first gives

SN−wSN=(1+w+w2+⋯+wN−1)−(w+w2+w3+⋯+wN)=1−wN,

because everything in the middle cancels out.

Now, we can factor out 1−w from the left hand side to get

(1−w)SN=1−wNSN=1−wN1−w∑k=0N−1wk=1−wN1−w.

◻
Referenced by (1 direct)

Direct references:

from More Series
Theorem \@{finite-sets-are-compact}

Every finite set is compact.

Proof \@{proof-of-finite-sets-are-compact}

Suppose K is a finite set in metric space X and that {Gα},α∈A is an open cover of K. Since K is finite, we can enumerate its points as {k1,…,kn}, for some n≥0. Then, for each i=1,…,n (there are none when n=0,) pick an α(i)∈A with xi∈Gα(i). Define the index set A0={α(1),…,α(n)}⊂A. Because n is finite, A0 is finite as well, and K={k1,…,kn}⊂⋃α∈A0Gα, so {Gα},α∈A0 is a finite sub-cover of the original open cover. Therefore, every open cover of K has a finite sub-cover, and K is compact.

◻
from Compact Sets
Theorem: First Simple Pole Residue Formula \@{first-simple-pole-residue-formula}

Resz=z0f(z)=b1=limz→z0(z−z0)f(z).

from Residue Integration
Theorem: Fourier Basis \@{fourier-basis}

Let N be a positive integer. Then the vectors

ϕn=(e2πink/N)k=0N−1

for n=0,…,N−1 form a basis for CN.

Proof \@{proof-of-fourier-basis}

To show linear independence, we will show a stronger condition, orthogonality, holds.

For m,n,k∈ZN,m≠n we can write that the kth entry of ϕm is

ϕm(k)=e2∗π∗iN(km(modN)),

and that the conjugate of the kth entry of ϕn is

ϕn(k)―=e2∗π∗iN(−kn(modN)).

Then, in our inner product between ϕm and ϕn, the kth term is

ϕm(k)ϕn(k)―=e2∗π∗iN(km(modN))e2∗π∗iN(−kn(modN))=e2∗π∗iN(k(m−n)(modN)).

Thus, for r=m−n(modN),

⟨ϕm,ϕn⟩=∑k=0N−1e2πiNkr.

Now we need to show that this sum is 0. Note that if we let w=e2πiNr, we can rewrite this as

⟨ϕm,ϕn⟩=∑k=0N−1wk.

From Finite Geometric Series, we have that

∑k=0N−1wk=1−wN1−w.

Substituting back in e2πiNr for w we get

∑k=0N−1e2πiNrk=1−e2πiNrN1−e2πiNr=1−1r1−e2πiNr=0.

Thus, ⟨ϕm,ϕn⟩=0, and so when m≠n, ϕm an ϕn are orthogonal and therefore @linearly-independent.

Now we need to show that ϕ0…ϕN−1 span CN.

Let u=(z0,z1,…,zN−1)∈CN. We need to find c0,c1,…,cN−1 such that

u=c0ϕ0+c1ϕ1+⋯+cN−1ϕN−1.

That is, we want constants c0⋯cN−1 such that

uu=∑n=0N−1cnϕn.

To find some specific cm, we can take the inner product of both sides with respect to ϕm to get

⟨u,ϕm⟩=⟨∑n=0N−1cnϕn,ϕm⟩.

@Linearity in the first argument of the inner product allows us to rewrite the right side to get

⟨u,ϕm⟩=∑n=0N−1cn⟨ϕn,ϕm⟩.

Now, we know that

⟨ϕn,ϕm⟩={N,n=m,0,n≠m.

so the inner product on the right-hand side is 0 except when n=m, and this reduces to

⟨u,ϕm⟩=cmN.

Therefore,

cm=⟨u,ϕm⟩N.

This shows that the Fourier basis described here indeed spans CN, and shows how to compute the Fourier coefficients c0…cN−1.

◻
from Discrete Fourier Transform
Theorem: Function of middle variable forms Markov Chain \@{function-of-middle-variable-forms-markov-chain}

Given Random Variables X,Y,Z if Z=f(Y), then X→Y →Z.

Proof \@{proof-of-function-of-middle-variable-forms-markov-chain}

If Z=f(Y), then Z is independent of X, so

p(y,z|x)=p(y|x,z)=p(y|x)p(z|y),

and then

p(x,y,z)=p(x)p(y|x)p(z|y).

◻
Referenced by (1 direct)

Direct references:

from Markov Chains
Theorem \@{function-is-continuous-at-point-iff-limit-at-point-equals-function-at-point}

Suppose X and Y are metric spaces, E⊂X,p∈E, with p a limit point of E, and f:E→Y. Then, f is continuous if and only if limx→pf(x)=f(p).

Proof \@{proof-of-function-is-continuous-at-point-iff-limit-at-point-equals-function-at-point}

Note that the definition of a function having a limit at point in a metric space is different from the definition of a function being continuous at a point in a metric space only in that the continuous definition requires the function to be defined at the point (and equal to the limit at the point.)

◻
from Continuity in Euclidean and Metric Spaces
Theorem \@{fundamental-theorem-of-line-integrals}

When a line integral is known to be independent of path, and its value is required along some curve with initial point A and final point B, we can either replace the given curve with a simpler curve, or, take the difference in the values of the function ϕ(x,y) at B and A.

∫CP(x,y)dx+Q(x,y)dy={ϕ(x,y)}AB=ϕ(xB,yB)−ϕ(xA,yA).

from Arc Length and Line Integrals
Theorem: Gibbs' Inequality \@{gibbs-inequality}

For discrete probability distributions p and q that share a support X,

D(p‖q)≥0,

with equality iff p=q. Equivalently, cross-entropy is never less than entropy: H(p,q)≥H(p), with equality iff q=p.

Proof \@{proof-of-gibbs-inequality}

Because Log is Concave, by Jensen's Inequality we have that

Ep[log⁡qipi]≤log⁡(Ep[qipi])=log⁡(∑i[piqipi])=log⁡(∑iqi)=log⁡1=0.

Then, since Ep[log⁡qipi]=−D(p‖q), we have that D(p‖q)≥0.

Now, note that if p=q, qipi=1 and D(p‖q)=0. Conversely, suppose D(p‖q)=0. Since log is strictly concave, it is not affine, and Jensen's Inequality condition for equality gives us that qipi=c. Now, ∑iqi=∑icpi=1, and since p is a probability distribution, c=1, and therefore pi=qi and p=q.

◻
Corollary: Nonnegativity of Mutual Information \@{nonnegativity-of-mutual-information}

For any two random variables, X,Y, I(X;Y)≥0, with equality if and only if X and Y are independent.

Proof \@{proof-of-nonnegativity-of-mutual-information}

Using the definition of mutual information and Gibbs' Inequality, we have I(X;Y)=D(p(x,y)‖p(x)p(y))≥0, with equality if and only if p(x,y)=p(x)p(y), i.e. X and Y are independent.

◻
Corollary: Nonnegativity of Conditional Relative Entropy \@{nonnegativity-of-conditional-relative-entropy}

D(p(y|x)‖q(y|x))≥0,

with equality if and only if p(y|x)=q(y|x) for all y and x such that p(x)>0.

Proof \@{proof-of-nonnegativity-of-conditional-relative-entropy}

From the definition of conditional relative entropy we have

D(p(y|x)‖q(y|x))=∑x∈Xp(x)∑y∈Yp(y|x)log⁡p(y|x)q(y|x)=∑x∈Xp(x)D(p(⋅|x)‖q(⋅|x)).

This is just the average of the relative-entropy over distributions over y for each fixed x. For p(x)>0, each is 0 if and only if p(y|x)=q(y|x), by Gibbs' Inequality, and positive otherwise.

◻
Corollary: Nonnegativity of Conditional Mutual Information \@{nonnegativity-of-conditional-mutual-information}

I(X;Y|Z)≥0,

with equality if and only if X and Y are conditionally independent given Z.

Proof \@{proof-of-nonnegativity-of-conditional-mutual-information}

We have that I(X;Y|Z)=∑z∈Zp(z)I(X;Y|Z=z),

and for each fixed z,

I(X;Y|Z=z)=D(p(x,y|z)‖p(x|z)p(y|z))≥0.

By Gibbs' Inequality, the quantity for each fixed z is non-negative, so the sum weighted by the probability of each z is also non-negative.

For equality, the average is 0 if and only if for each z with p(z)>0,

I(X;Y|Z=z)=0,

why by Gibbs' Inequality means

p(x,y|z)=p(x|z)p(y|z)

for all x,y, i.e. X and Y are conditionally independent given Z.

◻
Referenced by (5 direct)

Direct references:

from Discrete Entropy
from Vector Differential Calculus
Theorem \@{gradient-as-surface-normal-vector}

Let f be a differentiable scalar function in space. Let f(x,y,z)=c (with c constant) represent a surface S. Then, if the gradient of f at a point P of S is not the zero vector, it is a surface normal vector of S at P.

Proof \@{proof-of-gradient-as-surface-normal-vector}

Any curve C lying in S can be parameterized as r=[x(t),y(t),z(t)] such that

f(x(t),y(t),z(t))=c.(a)

Now, if we differentiate (a) with respect to t, we get

dfdt=∂f∂xx′+∂f∂yy′+∂f∂zz′=(gradf)⋅r′=0.

Therefore, gradf is orthogonal to all the vectors r′ in the tangent plane of S at P, and is therefore a surface normal vector of S at P.

◻
from Vector Differential Calculus
Theorem \@{gravitational-potential-is-a-solution-to-laplaces-equation}

The force of attraction

p=−cr3r=−c[x−x0r3,y−y0r3,z−z0r3]

between two particles at points P0=(x0,y0,z0) and P=(x,y,z) (as given by Newton's law of gravitation) has the potential function f(x,y,z)=c/r, where r>0 is the distance between P0 and P.

Thus, p=gradf=grad(c/r). This potential function f is a solution of Laplace's Equation

∇2f=∂2f∂x2+∂2f∂y2+∂2f∂z2=0,

that is, f has a Laplacian of 0.

from Vector Differential Calculus
Theorem: Green's Theorem \@{greens-theorem}

Suppose P(x,y) and Q(x,y) have continuous first partial derivatives in a domain containing a simple, closed, piecewise smooth curve C and its interior R. Then

∮CPdx+Qdy=∬R(∂Q∂x−∂P∂y)dxdy.

Referenced by (2 direct)

Direct references:

from Vector Integral Calculus
Theorem: Heine-Borel \@{heine-borel}

If a set E in Rk has one of the following three properties, then it has the other two:

(a) E is closed and bounded.

(b) E is compact.

(c) Every infinite subset of E has a limit point in E.

Proof \@{proof-of-heine-borel}

If (a) holds, then E⊂I for some k-cell I, and (b) follows from the facts that every k-cell is compact and closed subsets of compact sets are compact. Then, (c) follows from the fact that any infinite subset K of a compact set E has a limit point in E. To complete the cycle of implication, we must now show that (c) implies (a).

Assume, for the sake of contradiction, that E is not bounded. Then, E must contain an indexed set of points {xn},n=1,2,3,… where each xn must satisfy |xn|>n. {xn} is obviously infinite, but we will show it has no limit points in E. Let p∈E. Then for some positive integer N, |p|<N. Since N is finite, there can only be finitely many points {qα} in {xn} with |xn|<N. If {qα} is empty, then p is obviously not a limit point of {xn}. Otherwise, let r=min{d(p,qα)}. Then r>0 and let Nr{p} be a neighborhood of p. Since no point in {xn}, other than perhaps p, lies in {xn}, p is clearly not a limit point of {xn}. Thus, our provisional assumption is invalid and (c) implies E is bounded.

To show that (c) implies E is closed, assume for the sake of contradiction that E is not closed. Then, there is a point x0∈Rk which is a limit point of E but is not in E. We will construct an infinite subset of E and show that it has no limit point in E. For n=1,2,3,…, let the point xn be some point in E such that |xn−x0|<1/n; let {xn} be the set of such points. {xn} is certainly infinite, because |xn−x0| will eventually be bigger than 1/n for some n if we keep reusing the same xn infinitely many times. Now, {xn} has x0 as a limit point, and we will show it is its only limit point in Rk. Assume y∈Rk,y≠x0. Then, via the triangle inequality, |xn−y|≥|x0−y|−|xn−x0|≥|x0−y|−1n≥12|x0−y| for all but finitely many n, and thus y is not a limit point of {xn} because its its neighborhoods do not contain infinitely many points of {xn}. Thus, {xn} has no limit point in E, which contradicts (c), and therefore our provisional assumption that E is not closed is incorrect, and (c) implies that E is closed.

◻
Note \@{heine-borel-note}

Without proof here, (b) and (c) are equivalent in any metric space, but (a) does not imply (b) and (c) in every metric space (we assumed Rk above.)

Referenced by (5 direct)

Direct references:

from Compact Sets
Theorem \@{homomorphism-injective-iff-trivial-kernel}

One useful fact you may recall from linear algebra that also applies with group homomorphisms is that ϕ is injective iff the kernel of ϕ is {e}.

from Groups
Theorem \@{infinite-subset-has-limit-point-implies-compact}

Let X be a metric space in which every infinite subset has a limit point. Then X is compact.

Proof \@{proof-of-infinite-subset-has-limit-point-implies-compact}

By Let X be a metric space in..., we know that X is separable and by Every separable metric space has a countable..., we know that X has a countable base. By the definition of base, we have that every open cover of X has a countable subcover {Gn},n=1,2,3,….

Suppose, for the sake of contradiction, that {Gn} has no finite subcollection that covers X. Let

Fn=(G1∪⋯∪Gn)c.

Then, each Fn must be nonempty (otherwise a finite subcollection of {Gn} would cover X. However, since every point in X is in some Gn,

⋂n=1∞Fn=∅.

Now, let E be a set with a point from each Fn. Since there are infinitely many Fn, E is an infinite subset of X, and therefore E has a limit point, p. Now, p must be in some open Gm, and so for some ϵ>0, Nϵ(p)⊂Gm.

Now, note that each Fn+1⊂Fn, because Fn+1 is formed by excluding all the points in Fn that are also in Gn+1. Because p is a limit point of E, Nϵp must contain infinitely many points of E. However, only finitely many points of E can be in Nϵ(p)⊂Gm, because for n>=m, Fn contains no points in Gm. Therefore, p is not a limit point of E, and no such limit point can exist, contradicting our hypothesis that every infinite subset of X has a limit point. Therefore, E must be finite, and {Gn} must have a finite subcollection that covers X, meaning X is compact.

◻
from Perfect Sets and More
Theorem \@{infinite-subset-of-compact-set-has-limit-point}

If E is an infinite subset of a compact set K, then E has a limit point in K.

Proof \@{proof-of-infinite-subset-of-compact-set-has-limit-point}

Assume, for the sake of contradiction, that no point in K is a limit point of E. Then any point q in K has a neighborhood with at most one point in E; q, if q∈E. Since E is infinite, an infinite number of these singleton neighborhoods would be required to cover it, and therefore to cover K, since E⊂K. But, this contradicts our hypothesis that K is compact. Therefore, our provisional assumption must be false, and K must contain a limit point of E.

◻
Referenced by (3 direct)

Direct references:

from Compact Sets
Theorem \@{infinite-subset-of-countable-is-countable}

Every infinite subset E of a countably infinite set A is countable.

Proof \@{proof-of-infinite-subset-of-countable-is-countable}

Assume A is countably infinite, E⊂A, and |E|=∞. Arrange a sequence {xn} from the distinct elements of A. Let n1 be the smallest positive integer such that xn1∈E, and then pick n2,…,nk−1 by assigning the next n in the sequence the index of the left-most entry in {xn} that has not yet been picked. Then, let nk be the smallest integer greater than nk−1 such that xnk∈E. Now, {nk} is a sequence of strictly increasing positive integers giving us the indices of the first k elements of E in {xn}.

Now, define f:Z>0→E as f(k)=xkn, which is a bijection between the positive integers and E, showing that E is countable.

◻
Intuition \@{infinite-subset-of-countable-is-countable-intuition}

We can show this by putting A into a sequence {xn} of distinct values, so it can be indexed with the positive integers, and then constructing a subsequence of {xn} that are only the indices of elements of E.

As an example, consider the even numbers {0,2,4,…} as a subset of the non-negative integers {0,1,2,…}. Then, the indices of the even numbers are {1,3,5,…}, and f(1)=0,f(1)=2,….

Note \@{infinite-subset-of-countable-is-countable-note}

This means that countably infinite sets are the smallest infinite sets. Any infinite subset of one has the same cardinal number as the parent set, and the same cardinal number as the set of natural numbers - ℵ0 - "aleph null."

from Finite, Countable, and Uncountable Sets
Theorem \@{integral-of-one-over-z-around-unit-circle}

If C is the unit circle, then ∫C1zdz=2πi.

Proof \@{proof-of-integral-of-one-over-z-around-unit-circle}

First, note that we can parameterize C, the unit circle, as

z(θ)=eiθ,0≤θ<2π.

Now, making the substitution,

f(z(θ))=1e(iθ)=e−iθ.

Now, using the definition of the contour integral,

∫Cf(z)dz=∫αβf[z(t)]z′(t)dt

we have, noting that z′(θ)=ieiθ,

∫C1zdz=∫02πe−iθieiθdθ=i∫02πdθ=2πi.

◻
Referenced by (1 direct)

Direct references:

from Contour Integrals
Theorem: Intermediate Value Theorem \@{intermediate-value-theorem}

Suppose f:[a,b]→R is continuous and that r is a value between f(a) and f(b). Then there exists a number c in (a,b) for which f(c)=r.

from Continuity
Theorem \@{intersection-of-sequence-of-nested-intervals-is-nonempty}

If In is a sequence of intervals in R1, such that In+1⊂In,n=1,2,3,..., then ⋂i=1nIn is not empty.

Proof \@{proof-of-intersection-of-sequence-of-nested-intervals-is-nonempty}

Let In=[an,bn], and let E be the set of all an. Then, E is nonempty, because even if an=bn for all n, it at least contains a single point. It is also bounded above by b1, since any bn is in [a1,b1]. Let x=supE. Let m and n be positive integers and we have that an≤am+n≤bm+n≤bm, so that x≤bm for each m. Since am≤x, we have that am≤x≤bm, that is, x∈Im for all m=1,2,3,…, so x∈⋂i=1nIn and thus ⋂i=1nIn is not empty.

◻
Referenced by (1 direct)

Direct references:

from Compact Sets
Theorem \@{invariance-of-curl}

curlv is a vector. It has a length and a direction that are independent of the particular choice of a Cartesian coordinate system in space.

from Vector Differential Calculus
Theorem: Jensen's Inequality \@{jensens-inequality}

Let X be a random variable with finite expectation E[X], and let φ:R→R be a convex function. Then

φ(E[X])≤E[φ(X)].(a)

If φ is concave, the inequality reverses:

φ(E[X])≥E[φ(X)].

In either case, equality holds if and only if φ is affine on the support of X, or X is almost surely constant.

Proof \@{proof-of-jensens-inequality}

We will proceed by induction. Assume X is discrete and takes on n values x1,…,xn with probabilities p1,…,pn.

Base step, for n=2: Assume X takes on two distinct values, x1 and x2, with probabilities p1=λ,p2=1−λ. Then we want to show that

φ(E[X])≤E[φ(X)]φ(λx1+(1−λ)x2)≤λφ(x1)+(1−λ)φ(x2).

The last line is just the definition of a convex function, so it's obviously true.

Inductive step: Assume that (a) holds for any n−1 points. Take n points with weights pi summing to 1. Let

w=∑i=1n−1pi=1−pn.

Assuming w>0, let qi=pi/w. Then, qi>0,∑qi=1, so the qi form an (n−1)-point distribution. Now, we'll rewrite E[X] to bundle the first n−1 terms separately from the last term:

E[X]=∑i=1npixi=w∑i=1n−1qixi+pnxn=wx―+pnxn,(b)

where x―=∑i=1n−1qixi. Now, because w+pn=1, (b) is a two-point convex combination of x― and xn. From our base case,

φ(∑i=1npixi)=φ(wx―+pnxn)≤wφ(x―)+pnφ(xn).

Now, from our inductive hypothesis we have that

φ(x―)=φ(∑i=1n−1qixi)≤∑i=1n−1qiφ(xi).

Tying it all together we have

φ(E[X])=φ(∑i=1npixi)≤w∑i=1n−1qiφ(xi)+pnφ(xn)=∑i=1n−1piφ(xi)+pnφ(xn)=∑i=1npiφ(xi)=E[φ(X)].

TODO: show the equality case only holds when the support is affine.

◻
Referenced by (5 direct)

Direct references:

from Expectation
Theorem \@{joint-entropy-is-less-than-or-equal-to-entropy-of-parts}

Let X and Y be discrete random variables with alphabets X and Y, and let p(x,y) be the probability of the joint occurrence of X=x and Y=y.

The entropy of the joint event (the joint entropy), H(X,Y), is less than or equal to the sum of the individual entropies, i.e.

H(X,Y)≤H(X)+H(Y),

with equality iff X and Y are independent, that is, iff p(x,y)=p(x)p(y).

Proof \@{proof-of-joint-entropy-is-less-than-or-equal-to-entropy-of-parts}

The entropy of the joint event is

H(X,Y)=−∑x,yp(x,y)log⁡p(x,y).

This is just treating each possible pair of individual outcomes as its own outcome, i.e. we have |X|×|Y| possible outcomes. Writing p(x)=∑y′p(x,y′) and p(y)=∑x′p(x′,y) for the marginals (the argument names the distribution), we have

H(X)=−∑x,yp(x,y)log⁡∑y′p(x,y′),H(Y)=−∑x,yp(x,y)log⁡∑x′p(x′,y).

So,

H(X)+H(Y)−H(X,Y)=−∑x,yp(x,y)log⁡∑y′p(x,y′)−∑x,yp(x,y)log⁡∑x′p(x′,y)+∑x,yp(x,y)log⁡p(x,y)=∑x,yp(x,y)(log⁡p(x,y)−log⁡∑y′p(x,y′)−log⁡∑x′p(x′,y))=∑x,yp(x,y)(log⁡p(x,y)−log⁡p(x)−log⁡p(y))=∑x,yp(x,y)(log⁡p(x,y)p(x)p(y))=−∑x,yp(x,y)(log⁡p(x)p(y)p(x,y))

Now, let's define a new random variable for convenience, Z=p(X)p(Y)p(X,Y). We now have that

H(X)+H(Y)−H(X,Y)=−∑x,yp(x,y)(log⁡p(x)p(y)p(x,y))=−∑x,yp(x,y)(log⁡Z)=−E[log⁡Z].

Now, by Jensen's Inequality, because Log is Concave, we have that E[log⁡Z]≤log⁡E[Z]. Now,

E[Z]=∑x,yp(x,y)⋅p(x)p(y)p(x,y)=∑x,yp(x)p(y)=(∑xp(x))(∑yp(y))=1⋅1=1. Therefore log⁡E[Z]=log⁡1=0, and we have that E[log⁡Z]≤0⟹−E[log⁡Z]≥0, and

H(X)+H(Y)−H(X,Y)≥0−H(X,Y)≥−H(X)−H(Y)H(X,Y)≤H(X)+H(Y).

Now, for the equality part. Suppose H(X)+H(Y)=H(X,Y). Then, E[log⁡Z]=0, and recalling that E[Z]=1, E[log⁡Z]=log⁡E[Z]=0. In Jensen's Inequality, equality holds only if our function is affine or if Z is constant; since log is affine on no interval, Z must be constant, and since E[Z]=1, Z=p(x)p(y)p(x,y)=1⟹p(x)p(y)=p(x,y).

Now, suppose p(x)p(y)=p(x,y). Then Z=1 and

H(X)+H(Y)−H(X,Y)=−∑x,yp(x,y)(log⁡1)=0,

so H(X)+H(Y)=H(X,Y).

◻
Referenced by (1 direct)

Direct references:

from Discrete Entropy
Theorem: L'Hospital \@{lhospital}

Suppose there is a δ>0 such that f and g are differentiable on (c−δ,c+δ) with g′(x)≠0 on this interval. Suppose also that

limx→cf′(x)g′(x)=L.

Then if limx→cf(x)=limx→cg(x)=0, limx→cf(x)=limx→cg(x)=∞, or limx→cf(x)=limx→cg(x)=−∞, we have that

limx→cf(x)g(x)=L.

The endpoint c can also be ±∞.

from Differentiation
Theorem \@{lagrange-theorem-for-indices}

Suppose H and K are subgroups of a group G such that K≤H≤G, and suppose that (H:K) and (G:H) are both finite. Then (G:K)=(G:H)(H:K) is finite.

Intuition \@{lagrange-theorem-for-indices-intuition}

The intuition here is that each coset of H can be partitioned into (H:K) cosets of K, and that G can be partitioned into (G:H) cosets of H, so G can be partitioned into (G:K)=(G:H)(H:K) cosets of K. Since both (G:H) and (H:K) are given as finite, their product is also finite.

Proof \@{proof-of-lagrange-theorem-for-indices}

In more detail, say G can be partitioned into n=(G:H) cosets of H, where n is a natural number. Let A be a set of coset representatives A⊆G such that P=⋃ai∈AaiH is a partition of G formed by the left cosets of H.

Then, P is

P={a1H,a2H,a3H,⋯,anH},(a)

and each aiH is a disjoint coset of H in G.

Now, H can be partitioned into m=(H:K) cosets of K, where m is a natural number. Let B be a set of coset representatives B⊆H such that Q=⋃bi∈BbiK is a partition of H formed by the left cosets of K.

Then, Q={b1K,b2K,b3K,⋯,bmK}. Now, we can recover H by taking the union of the elements of Q, that is, H=⋃q∈Qq, so the elements of Q, after a round of flattening, are the same as those of H. If we replace H in (a) with Q, distribute each an group action over the elements of Q, and then take the union across each resulting set we end up with

R={a1b1K,a1b2K,a1b3K,⋯,a1bmK,a2b1K,a2b2K,a2b3K,⋯,a2bmK,a3b1K,a3b2K,a3b3K,⋯,a3bmK,⋯,anb1K,anb2K,anb3K,⋯,anbmK},

which is G partitioned into the left cosets of K. Because we constructed each element in R by partitioning the elements of a partition of G into cosets of K (then taking their union), we know they are disjoint and cover all of G. There are nm=(G:H)(H:K)=(G:K) elements in R, and since n and m are finite, so is (G:K).

◻
from Groups
Theorem: Large-Sample Confidence Interval for a Proportion \@{ci-proportion}

If p^ is the proportion of successes in a random sample of size n and q^=1−p^, an approximate 100(1−α)% confidence interval for the binomial parameter p is given by

p^−zα/2p^q^n<p<p^+zα/2p^q^n.

Note \@{ci-proportion-note}

When n is small and the unknown proportion p is believed to be close to 0 or 1, this approach doesn't work well and shouldn't be used. This approach should only be used when both np^ and nq^ are greater than or equal to 5.

from Confidence Intervals
Theorem: Law of Large Numbers \@{law-of-large-numbers}

Suppose X1,X2,… are independent and identically distributed random variables with finite @mean μ. Then for any ϵ>0,

limn→∞P(|X1+⋯+Xnn−μ|≥ϵ)=0.

Note \@{law-of-large-numbers-note}

Intuitively, this means that the more identically distributed random variables we have, the closer their average value will get to the mean for the random variables. If we think of each random variable as an identical sample from the same population, another way to think of this is the more samples we get, the closer the average value across all samples will be to the true average value for the population, and we can get as close as we like to the true average value for the population by taking more samples.

Proof \@{proof-of-law-of-large-numbers}

We assume that the variance of the random variables is also finite. Then, note that

E[X1+⋯Xnn]=μ,

and

V[X1+⋯Xnn]=σ2n.

Then, by Chebyshev's Inequality, we have

P(|X1+⋯+Xnn−μ|≥ϵ)≤σ2nϵ2.

Now, as n increases, the term on the right approaches 0, which by the Squeeze Theorem implies the term on the left also approaches 0, and is 0 at the limit. ◻

◻
from Limit Theorems
Lemma \@{lemma-93}

TODO: Cover & Thomas Lemma 2.10.1. Proof by Jensen. If X and X′ are i.i.d. with entropy H(X), then

Pr(X=X′)≥2−H(X),

with equality if and only if X has a uniform distribution.

Proof \@{proof-of-lemma-93}

Suppose that X∼p(x). By Jensen's Inequality we have

2E[log⁡p(X)]≤E[2log⁡p(X)],

which implies that

2−H(X)=2∑p(x)log⁡p(x)≤∑p(x)2log⁡p(x)=∑p2(x).

◻
Corollary \@{corollary-95}

Let X,X′ be independent with X∼p(x), X′∼r(x), x,x′∈X. Then

Pr(X=X′)≥2−H(p)−D(p‖r), Pr(X=X′)≥2−H(r)−D(r‖p).

Proof \@{proof-of-corollary-95}

Note that

2−H(p)−D(p‖r)=2∑p(x)log⁡p(x)+∑p(x)log⁡r(x)p(x)=2∑p(x)log⁡r(x)≤∑p(x)2log⁡r(x)=∑p(x)r(x)=Pr(X=X′),

where the inequality follows from Jensen's Inequality and the fact that f(y)=2y is a convex function.

◻
from Discrete Entropy
Theorem \@{limit-of-a-function-characterized-by-limits-of-sequences}

Let X and Y be metric spaces; suppose E⊂X, f:E→Y, and p is a limit point of E. Then

limx→pf(x)=q(a)

if and only if

limn→∞f(pn)=q(b)

for every sequence {pn} in E such that

pn≠p,limn→∞pn=p.(c)

Proof contrapositive \@{proof-of-limit-of-a-function-characterized-by-limits-of-sequences}

Suppose that (a) is true and let {pn}⊂E be a sequence such that (c) holds. Let ϵ>0. Then, for some δ>0, if dX(x,p)<δ, then dY(f(x),q)<ϵ. Now, there is also some N such that dX(pn,p)<δ whenever n≥N, and thus, dY(f(pn),q)<ϵ whenever n≥N, so (b) holds.

Conversely, suppose that (a) is false. Then, for some ϵ>0, that for every δ>0 there exists a point x∈E such that dY(f(x),q)≥ϵ but 0<dX(x,p)<δ. If we let δn=1/n,n=1,2,3,…, and each xn a point such that 0<dX(xn,p)<δn, then {xn} is a sequence satisfying (c). However, since dY(f(xn),q)≥ϵ for all n, (b) does not hold.

◻
Corollary \@{limit-of-a-function-at-a-point-is-unique-if-it-exists}

If f has a limit at p, this limit is unique.

Proof \@{proof-of-limit-of-a-function-at-a-point-is-unique-if-it-exists}

This follows directly from the facts that limits of sequences are unique and that limits of functions are characterized by limits of sequences.

◻
Referenced by (2 direct)

Direct references:

from Continuity in Euclidean and Metric Spaces
Theorem \@{limit-of-diameter-of-remaining-points-in-cauchy-sequence-is-zero}

if {pn} is a sequence in X and if EN consists of the points pN,pN+1,pN+2,…, then {pn} is a Cauchy sequence if and only if

limN→∞diamEN=0.

Proof \@{proof-of-limit-of-diameter-of-remaining-points-in-cauchy-sequence-is-zero}

Suppose {pn} is a Cauchy sequence. Then, let ϵ>0. For some integer N, d(pn,pm)<ϵ when n,m≥N. Therefore, diamEN<ϵ. Since ϵ was arbitrary, we can see that the sequence {diamEN} converges to 0.

Conversely, suppose limN→∞diamEN=0. Then, every neighborhood of 0 contains {diamEN} for all but finitely many N. Let ϵ>0. Then, pick N such that diamEn<ϵ. Letting m,n≥N, we have that d(pm,pn)≤diamEn<ϵ.

◻
Referenced by (1 direct, 1 transitive)

Direct references:

Transitive (depth 1):

from Sequences in Euclidean and Metric Spaces
Theorem \@{limit-point-implies-convergent-sequence}

If E⊂X and if p is a limit point of E, then there is a sequence {pn} in E such that p=limn→∞pn.

Proof \@{proof-of-limit-point-implies-convergent-sequence}

For each n=1,2,3…, there is a point pn∈E such that d(p,pn)<1/n. Let ϵ>0, and pick N so that Nϵ>1. Then, if n>N, d(p,pn)<ϵ, so limn→∞pn=p.

◻
from Sequences in Euclidean and Metric Spaces
Theorem \@{limit-points-form-closed-set}

Let E′ be the set of all limit points of a set E in space X. Then E′ is closed.

Proof \@{proof-of-limit-points-form-closed-set}

Let p∈X,p∉E′. Then some neighborhood N of p contains no points in E, other than possibly p itself. If N contains only p, then p is not a limit point of E′. Suppose, for the sake of contradiction, some point q∈N,q≠p is a limit point of E′. Then, every neighborhood of q contains some point m in E′. Let M⊂N,p∉M, be such a neighborhood, and let m∈M,m≠q be a limit point of E. Now, m has neighborhoods wholly in N, and such neighborhoods can have no point in E, so we have a contradiction, and therefore q is not a limit point of E′. Hence, p is an interior point of E′c, and E′c is open, and therefore E′ is closed.

◻
from Metric Spaces
Theorem \@{limits-of-sequences-are-unique}

If p∈X,p′∈X and {pn} converges to p and p′, then p=p′.

Proof \@{proof-of-limits-of-sequences-are-unique}

Suppose, for contradiction, that p≠p′. Then, ϵ=d(p,p′)>0. Let δ=ϵ/2 and Bδ(p),Bδ(p′) be balls around p and p′, respectively. This means that only finitely many points from {pn} are not in Bδ(p). However, since Bδ(p) and Bδ(p′) are disjoint by construction, this means only finitely many points of {pn} are in Bδ(p′), a contradiction. Therefore, our assumption that p≠p′ is incorrect, so p=p′.

◻
Referenced by (2 direct)

Direct references:

from Sequences in Euclidean and Metric Spaces
Theorem \@{line-integral-over-a-plane-curve}

If f is a continuous function of two variables x=x(t),y=y(t) whose domain includes the smooth curve C, then the line integral can be evaluated as:

∫Cf(x,y)ds=∫abf(x(t),y(t))(dxdt)2+(dydt)2dt

from Arc Length and Line Integrals
Theorem \@{linear-stability-analysis}

Let x∗ be a fixed point of x˙=f(x). Then, if f′(x)≠0, if f′(x∗) is negative, then x∗ is a stable fixed point . If f′(x∗) is positive, then x∗ is an unstable fixed point.

Remark \@{linear-stability-analysis-remark}

This comes from letting u(t)=x(t)−x∗ be a small perturbation away from x∗, differentiating it, writing its taylor series, then noticing that f(x∗)=0 and terms greater than the linear term matter less than the linear term and writing

u˙=f′(x∗)u.

This is called the linearization about x∗.

It also only works if f′(x)≠0. If that's not the case, the best bet is to fall back to graphical analysis or to solve explicitly if possible.

from Flows on the Line
Theorem: Log is Concave \@{log-is-concave}

The log function is concave, i.e. −log is convex.

Proof \@{proof-of-log-is-concave}

The second derivative of natural log is −1x2, which is always non-positive. By Second Derivative Test for Convexity, log is therefore concave.

◻
Referenced by (2 direct)

Direct references:

from Logarithms
Theorem: Log Sum Inequality \@{log-sum-inequality}

For non-negative numbers, a1,a2,…,an and b1,b2,…,bn,

∑i=1nailog⁡aibi≥(∑i=1nai)log⁡(∑i=1nai∑i=1nbi),

with equality if and only if aibi=const.

We use the conventions that 0log⁡0=0,alog⁡a0=∞ if a>0, and 0log⁡00=0, all of which follow from @continuity.

Proof \@{proof-of-log-sum-inequality}

We can assume without loss of generality, due to the 0-handling conventions specified above, that ai>0 and bi>0. Now, note that the function f(t)=tlog⁡t is @strictly convex, since f″(t)=1tlog⁡e>0 for all positive t. Then, by Jensen's Inequality we have

∑αif(ti)≥f(∑αiti).

as long as αi>0,∑iαi=1, i.e. if the αi form a @discrete probability distribution.

If we let αi=bi∑j=1nbj, i.e. αi is the @probability mass assigned to index i, then this condition is met. We can then pick ti=aibi and we get

∑i=1nαif(ti)≥f(∑i=1nαiti)⟺∑i=1nαitilog⁡ti≥(∑i=1nαiti)log⁡(∑i=1nαiti)⟺∑i=1nbi∑j=1nbjaibilog⁡aibi≥(∑i=1nbi∑j=1nbjaibi)log⁡(∑i=1nbi∑j=1nbjaibi)⟺∑i=1nai∑j=1nbjlog⁡aibi≥(∑i=1nai∑j=1nbj)log⁡(∑i=1nai∑j=1nbj)⟺1∑j=1nbj∑i=1nailog⁡aibi≥1∑j=1nbj(∑i=1nai)log⁡(∑i=1nai∑i=1nbj)⟺∑i=1nailog⁡aibi≥(∑i=1nai)log⁡(∑i=1nai∑i=1nbj).

◻
Referenced by (2 direct)

Direct references:

from Discrete Entropy
Theorem: Logarithm Change of Base \@{logarithm-change-of-base}

logb⁡(a)=logx⁡(a)logx⁡(b).

Proof \@{proof-of-logarithm-change-of-base}

By definition,

◻
Referenced by (1 direct)

Direct references:

from Logarithms
Theorem \@{mapping-continuous-iff-inverse-images-of-open-sets-are-open}

A mapping f of a metric space X into a metric space Y is continuous on X if and only if f−1(V) is open in X for every open set V in Y (see inverse image.)

Proof \@{proof-of-mapping-continuous-iff-inverse-images-of-open-sets-are-open}

Assume f is continuous on X and V is an open set in Y. Suppose, for the sake of contradiction, that f−1(V) is not open. Then, some point p∈f−1(V) is not an interior point of f−1(V), which means there is no neighborhood of p that contains only points in f−1(V), that is, every neighborhood of p contains some point q that is not in f−1(V), i.e., f(q)∉V. Now, since V is open and f(p)∈V, there is some ϵ>0 for which Bϵ(f(p))⊂V, but, since all neighborhoods of p contain some q∉f−1(V), there is no δ>0 for which all points within δ of p are mapped to Bϵ(f(p)) by f, a contradiction, since f is continuous on X by hypothesis. Therefore, our assumption is incorrect and f−1(V) is open.

Conversely, suppose f−1(V) is open in X for every open set V in Y. Let V be an open set in Y. Assume, for the sake of contradiction that there is some p∈f−1(V) at which f is not continuous. Let ϵ>0. Then, there is no δ>0 for which Bδ(p) contains only points that are mapped by f to V, i.e. every neighborhood of p contains some point that is not in f−1(V), and therefore p is not an interior point of f−1(V), and f−1(V) is not open, a contradiction. Thus, our assumption must be incorrect, and there is no such p, and since entire space Y is an open subset of itself, f must be continuous on all of X.

◻
Corollary \@{mapping-continuous-iff-inverse-images-of-closed-sets-are-closed}

A mapping f of a metric space X into a metric space Y is continuous on X if and only if f−1(C) is closed in X for every closed set C in Y.

Proof \@{proof-of-mapping-continuous-iff-inverse-images-of-closed-sets-are-closed}

First, note that for any E⊂Y, we have f−1(Ec)=f−1(E)c, since x∈f−1(Ec) exactly when f(x)∉E, which is exactly when x∉f−1(E).

Now, as V ranges over the open subsets of Y, its complement Vc ranges over the closed subsets of Y, by A set E is open iff its.... So, by A mapping f of a metric space..., f is continuous on X if and only if f−1(Cc) is open in X for every closed set C in Y. By the observation above, f−1(Cc)=f−1(C)c, and this is open in X if and only if f−1(C) is closed in X, again by A set E is open iff its....

◻
Referenced by (1 direct)

Direct references:

Referenced by (1 direct)

Direct references:

from Continuity in Euclidean and Metric Spaces
Theorem: Markov's Inequality \@{markovs-inequality}

Let X be a non-negative random variable (X≥0,) and t>0. Then,

P(X≥t)≤E[X]t.

Note \@{markovs-inequality-note}

That is, the probability that X is at least t has an upper-bound of the expectation (mean) of X divided by t. In simpler terms, the probability that X>t can't be too big.

Note that as t grows larger, the probability of X being greater than t grows smaller.

Proof \@{proof-of-markovs-inequality}

This follows from the Law of Total Expectation, which is

E[X]=E[X∣X≥t]P(X≥t)+E[X∣X<t]P(X<t).(a)

Here, we're partitioning X's sample space into a portion above t and a portion below t.

Now, E[X∣X≥t] is the expected value when X≥t, which is necessarily at least t, since X is restricted to taking on values of at least t. So, we have that E[X∣X≥t]≥t.

We can substitute this into (a) to get

E[X]≥tP(X≥t)+E[X∣X<t]P(X<t).(b)

Note that our equation has turned into an inequality; we must do this because the original RHS was equal to the original LHS, and the original RHS is greater than or equal to our new RHS, which means the original LHS is greater than or equal to our new RHS.

Now, since we said that X is non-negative, its expected value is also non-negative, including when X<t. We have by definition that P(X<t) is non-negative (because all probabilities are non-negative). Therefore, E[X∣X<t]P(X<t) must also be non-negative as it's the product of two non-negative numbers. Since the LHS of (b) is greater than the RHS with this non-negative value added to the RHS, the LHS is also bigger without it added, and therefore we can drop it to get

E[X]≥tP(X≥t)(c)

Dividing both sides by t and swapping sides gives us

P(X≥t)≤E[X]t.◻

◻
Referenced by (4 direct)

Direct references:

from Limit Theorems
Theorem: Mean Value Inequality for Vector Valued Functions \@{mean-value-inequality-for-vector-valued-functions}

Suppose f:[a,b]→Rd is continuous on [a,b] and differentiable on (a,b). Then there exists x∈(a,b) such that ‖f(b)−f(a)‖≤(b−a)‖f′(x)‖.

Proof \@{proof-of-mean-value-inequality-for-vector-valued-functions}

Let z=f(b)−f(a), and define φ(t)=⟨z,f(t)⟩,(a≤t≤b). If z=0, then the result is trivial and we're done, so assume z≠0. Then φ is a real valued continuous function on [a,b] and is differentiable on (a,b). By the Mean Value Theorem, there is some x∈(a,b) such that φ(b)−φ(a)=(b−a)φ′(x)=(b−a)⟨z,f′(x)⟩. On the other hand, φ(b)−φ(a)=⟨z,f(b)⟩−⟨z,f(a)⟩=⟨z,f(b)−f(a)⟩=⟨z,z⟩=‖z‖2. Now, by the Cauchy-Schwarz Inequality, ‖z‖2=(b−a)|⟨z,f′(x)⟩|≤(b−a)‖z‖‖f′(x)‖. Therefore, ‖z‖≤(b−a)‖f′(x)‖, which is what we wanted to show.

◻
Referenced by (1 direct)

Direct references:

from Differentiation
Theorem: Mean Value Theorem \@{mean-value-theorem}

Suppose f is continuous on [a,b] and differentiable on (a,b). Then there exists a point c in (a,b) such that:

f′(c)=f(b)−f(a)b−a.

This means that for a function continuous on an interval, and differentiable on that interval except maybe at its endpoints, there is a point on the interval where the derivative of the function at that point equals the slope of the function between its endpoints.

Referenced by (2 direct)

Direct references:

from Differentiation
Theorem: Moment Generating Function of a Sum \@{mgf-of-sum}

The moment generating function for the sum of two random variables is the product of the moment generating functions of the two random variables. More generally, if X1,X2,…Xn are independent random variables, then

MX1+X2+⋯+Xn(t)=MX1(t)⋅MX2(t)⋯MXn(t).

Proof \@{proof-of-mgf-of-sum}

We'll prove the case where n=2; the general proof is exactly the same but more tedious.

MX+Y(t)=E[et(X+Y)]=E[etXetY]=E[etX]E[etY]=MX(t)MY(t).◻

◻
from Limit Theorems
Theorem: Multiplication Rule for Distributions \@{joint-is-marginal-times-conditional}

TODO: state f(x,y)=fX(x)fY|X(y|x)=fY(y)fX|Y(x|y), and the n-variable chain rule f(x1,…,xn)=∏i=1nf(xi|xi−1,…,x1). Note it reduces to a product distribution when the variables are independent.

Proof \@{proof-of-joint-is-marginal-times-conditional}

TODO: rearrange the definition of conditional probability distribution; induct for the n-variable form.

◻
Referenced by (1 direct)

Direct references:

from Joint Probability
Theorem: Mutual Information and Entropy \@{mutual-information-and-entropy}

I(X;Y)=H(X)−H(X|Y)(a)I(X;Y)=H(Y)−H(Y|X)(b)I(X;Y)=H(X)+H(Y)−H(X,Y)(c)I(X;Y)=I(Y;X)(d)I(X;X)=H(X).(e)

Proof \@{proof-of-mutual-information-and-entropy}

We'll prove (c) first:

I(X;Y)=∑x∈X∑y∈Yp(x,y)log⁡p(x,y)p(x)p(y)=∑x∈X∑y∈Yp(x,y)(log⁡p(x,y)−log⁡p(x)p(y))=−H(X,Y)−∑x∈X∑y∈Yp(x,y)log⁡p(x)p(y)=−H(X,Y)−∑x∈X∑y∈Yp(x,y)(log⁡p(x)+log⁡p(y))=−H(X,Y)−∑x∈X∑y∈Yp(x,y)log⁡p(x)−∑x∈X∑y∈Yp(x,y)log⁡p(y)=H(X)+H(Y)−H(X,Y)

Now, from Chain rule for joint entropy we prove (a) and (b) with

H(X)+H(Y)−H(X,Y)=H(X)+H(Y)−H(Y)−H(X|Y)=H(X)−H(X|Y).

and

H(X)+H(Y)−H(X,Y)=H(X)+H(Y)−H(X)−H(Y|X)=H(Y)−H(Y|X).

(d) is trivial from symmetry of p(a,b)=p(b,a) and a∗b=b∗a.

To prove (e) we use our result from (a): I(X;X)=H(X)+H(X)−H(X,X)=H(X)+H(X)−H(X)=H(X).

◻
Referenced by (1 direct)

Direct references:

from Discrete Entropy
Theorem \@{n-tuples-of-countable-elements-are-countable}

Let A be a countable set, and let Bn be the set of all n-tuples (a1,…,an) where ak∈A(k=1,…,n), and the elements a1,…,an need not be distinct. Then Bn is countable.

Proof \@{proof-of-n-tuples-of-countable-elements-are-countable}

We will proceed using proof by induction. First, for the base case, note that B1 is the set of 1-tuples formed by elements of A, so B1=A and is thus countable. Now, for the inductive step, assume Bn−1 is countable (n=2,3,4,…). Then we have that

Bn={(b,a)|b∈Bn−1,a∈A}=⋃b∈Bn−1(b×A).

So, for any given n−1-tuple b, we form n-tuples by appending each element of a to it, and so the set of pairs (b,a) has the same cardinality as A, and is thus countable. Bn is thus the union of the countable set of countable sets (the set of sets formed by appending each element of A to each element of Bn−1) and is therefore countable itself, by a theorem proved above. Therefore, by induction, every Bn is countable.

◻
Corollary \@{rationals-are-countable}

The set of rational numbers is countable.

Proof \@{proof-of-rationals-are-countable}

Rational numbers just formed from pairs of integers: (a,b)→a/b,b≠0, so we use the above theorem with n=2.

◻
Referenced by (3 direct)

Direct references:

Referenced by (1 direct)

Direct references:

from Finite, Countable, and Uncountable Sets
Theorem \@{negation-of-conjunction-is-disjunction-of-negations}

The negation of a conjunction is the disjunction of negations.

Proof \@{proof-of-negation-of-conjunction-is-disjunction-of-negations}

Let A and B be boolean variables. We want to show that

¬(A∧B)↔¬A∨¬B.

First, assume ¬(A∧B) is true. Then, both A∧B must be false, so either A must be false or B must be false, or both must be false. If A is false, then ¬A is true, and so is ¬A∨¬B. The same is true if B is false, so ¬(A∧B)→¬A∨¬B.

Now, assume ¬A∨¬B is true. Then, either ¬A or ¬B must be true, so either A or B or both must be false. Now, if A is false, then A∧B is false. The same holds if B is false, and thus ¬(A∧B) is true. Therefore ¬A∨¬B→¬(A∧B) and we have shown ¬(A∧B)↔¬A∨¬B.

◻
from Boolean Algebra
Theorem \@{negation-of-disjunction-is-conjunction-of-negations}

The negation of a disjunction is the conjunction of negations.

Proof \@{proof-of-negation-of-disjunction-is-conjunction-of-negations}

Let A and B be boolean variables. We want to show that

¬(A∨B)↔¬A∧¬B.

First, assume ¬(A∨B) is true. Then, A∨B is false. If A were true, then we'd have a contradiction, and similarly with B, so both A and B must be false, that is, ¬A and ¬B most both be true, and ¬(A∨B)→¬A∧¬B.

Now, assume ¬A∧¬B. Here, both ¬A and ¬B must be true, so both A and B must be false. Therefore, A∨B is false, so ¬A∧¬B→¬(A∨B) and we have shown ¬(A∨B)↔¬A∧¬B.

◻
from Boolean Algebra
Theorem \@{neighborhood-of-limit-point-contains-infinitely-many-points}

If p is a limit point of a set E, then every neighborhood of p contains infinitely many points of E.

Proof \@{proof-of-neighborhood-of-limit-point-contains-infinitely-many-points}

Let p be a limit point of E and let Nr(p) be a neighborhood of p. Suppose that Nr(p) contains only finitely many points of E. Since we have finitely many points, we can inspect each and find the minimum distance from p to any point in Nr(p)⋃E∖{p} and call it s. Now, we can make a new neighborhood Ns(p), which contains none of the points in Nr(p)⋃E∖{p} since they're all at least s away from p, by construction. But then, p is not a limit point of E, since it has a neighborhood that contains no points of E∖{p} Therefore, we have a contradiction, and Nr(p) must therefore contain infinitely many points.

◻
Corollary \@{only-infinite-sets-have-limit-points}

From this, it's evident that a finite set of points has no limit points. That is, if a set has a limit point, then the set if infinite.

Referenced by (2 direct)

Direct references:

Referenced by (3 direct)

Direct references:

from Metric Spaces
Theorem \@{nested-sequence-of-compact-sets-with-lim-diam-zero-has-singleton-intersection}

If Kn is a sequence of nonempty compact sets in X such that Kn+1⊂Kn,(n=1,2,3,…) and if

limn→∞diamKn=0,

then ⋂1∞Kn consists of exactly one point.

Proof \@{proof-of-nested-sequence-of-compact-sets-with-lim-diam-zero-has-singleton-intersection}

Let K=⋂1∞Kn. Then K is not empty. Assume for the sake of contradiction that K contains more than one point. Then, diamK>0. But, for each n,K⊂Kn, so that diamKn≥diamK. But, this contradicts our given that lim+n→∞diamKn=0, so our assumption that K contains more than one point must be invalid, and thus K contains exactly one point.

◻
Referenced by (1 direct, 1 transitive)

Direct references:

Transitive (depth 1):

from Sequences in Euclidean and Metric Spaces
Theorem: Noiseless channel transmitting discrete symbols \@{noiseless-channel-transmitting-discrete-symbols}

Given a communication channel which has a capacity of C bits per second, accepting signals from a source of entropy (or information) of H bits per symbols, it is possible, given a properly devised coding procedure, for the transmitter to transmit symbols over the channel at an average rate which is nearly C/H but which, no matter how clever the coding, can never exceed C/H.

from Entropy of a Discrete Information Source
Theorem \@{non-empty-perfect-sets-in-rk-are-uncountable}

Let P be a nonempty perfect set in Rk. Then P is uncountable.

Proof \@{proof-of-non-empty-perfect-sets-in-rk-are-uncountable}

We know that P is infinite, because by definition, all points in perfect sets are limit points, and only infinite sets have limit points.

Suppose, for the sake of contradiction, that P is countable. Label the points of P as x1,x2,…. We will construct a sequence of Vn of neighborhoods.

As a base step, let V1 be any neighborhood of x1; let V1={y∈Rk| |y−x1|<r} (note: subsequent Vn+1 aren't required to be neighborhoods of xn+1.) Then the closure V1― of V1 is V1―={y∈Rk| |y−x1|≤r}.

For the inductive step, suppose as an induction hypothesis that we have some Vn that's been constructed such that Vn∩P is not empty. Since every point of P is a limit point of P, we can make a neighborhood Vn+1 such that (i) Vn+1―⊂Vn, (ii) xn∉Vn+1―, (iii) Vn+1∩P is not empty. Now, Vn+1 satisfies our induction hypothesis, and since V1 does too, we have Vn defined for all n=1,2,3,….

For each n, let Kn=Vn―∩P. Since Vn― is closed and bounded, Vn― is compact. Since xn∉Vn+1―, no point of P lies in ⋂n=1∞Kn. Since Kn⊂P, this implies that ⋂n=1∞Kn is empty. But, each Kn is nonempty, by (iii), and Kn+1⊂K, by (i). But the intersection of nonempty compact nested sets is nonempty, so we have a contradiction, so our provisional assumption that P is countable must be incorrect. Therefore, P is uncountable.

◻
Corollary \@{every-interval-is-uncountable}

Every interval [a,b](a<b) is uncountable, and thus the set of all real numbers is uncountable as it contains uncountable subsets.

Referenced by (1 direct)

Direct references:

Referenced by (2 direct)

Direct references:

from Perfect Sets and More
Theorem: Nonadditivity of outer measure \@{nonadditivity-of-outer-measure}

There exist @disjoint subsets A and B or R such that

|A∪B|≠|A|+|B|.

Note \@{nonadditivity-of-outer-measure-note}

The proof of this theorem uses Vitali Sets.

Referenced by (1 direct)

Direct references:

from Outer Measure
Theorem \@{nonempty-intersection-of-finitely-many-compact-sets}

If {Kα} is a collection of compact subsets of a metric space X such that the intersection of every finite subcollection of {Kα} is nonempty, then ⋂Kα is nonempty.

Proof \@{proof-of-nonempty-intersection-of-finitely-many-compact-sets}

Let Gα=Kαc for each α, and note that since Kα is compact and therefore closed, Gα is open. Then, fix a member K1 of {Kα}. Assume, for contradiction's sake, that no point of K1 is in all Kα, that is, that ⋂Kα=∅. Then, any point x∈K1 is in some Kαc=Gα, so {Gα} forms an open cover of K1. Since K1 is compact, some finite subset Gα1,…,Gαn of {Gα} forms a finite subcover of K1 such that K1⊂Gα1∪⋯∪Gαn=(Kα1∩⋯∩Kαn)c (by De Morgan's.) Therefore K1∩Kα1∩⋯∩Kαn=∅. This is an empty intersection of a finite subcollection of {Kα}, which contradicts our hypothesis that all finite intersections are nonempty. Therefore, our assumption that no point in K1 is in all Kα is incorrect, and some point in K1 is in all Kα, and therefore ⋂Kα is not empty.

◻
Corollary \@{intersection-of-nonempty-nested-compact-sets-is-nonempty}

If {Kα} is a sequence of nonempty compact sets such that Kn+1⊂Kn,n=1,2,3,…, then ⋂i=1∞Kn is not empty.

Proof \@{proof-of-intersection-of-nonempty-nested-compact-sets-is-nonempty}

Suppose x∈Kn,n≥2. Then, by definition, x∈Kn−1, and by induction, x∈K1. Then, every Kα is a nonempty subset of K1, and so the intersection of any finite number of these Kα will be nonempty, and by If {Kα} is a collection of compact..., ⋂i=1∞Kn is not empty.

◻
Referenced by (2 direct)

Direct references:

Referenced by (1 direct)

Direct references:

from Compact Sets
Theorem: nonexistence of extension of length to all subsets of R \@{nonexistence-of-extension-of-length-to-all-subsets-of-reals}

There does not exist a function μ with all of the following properties:

  1. (a) μ is a function from the set of subsets of R to [0,∞].
  2. (b) μ(I)=ℓ(I) for every @open interval I of R.
  3. (c) μ(⋃k=1∞Ak)=∑k=1∞μ(Ak) for every @disjoint sequence A1,A2,… of subsets of R.
  4. (d) μ(t+A)=μ(A) for every A⊂R and every t∈R.
Proof \@{proof-of-nonexistence-of-extension-of-length-to-all-subsets-of-reals}

Outline: assume such a μ exists. Then we can show that it has all of the properties of outer measure that were used to prove Nonadditivity of outer measure, but this means μ doesn't satisfy (c), a contradiction. TODO: full proof from paper notes.

◻
from Measurable Spaces and Functions
Lemma: Nonnegativity of Entropy \@{nonnegativity-of-entropy}

H(X)≥0.

Proof \@{proof-of-nonnegativity-of-entropy}

0≤p(x)≤1⟹log⁡p(x)≤0⟹−log⁡p(x)≥0.

◻
from Discrete Entropy
Theorem: Nonnegativity of Relative Entropy \@{nonnegativity-of-relative-entropy}

For discrete probability distributions p and q that share a support X,

D(p‖q)≥0,

with equality if and only if p=q.

Proof \@{proof-of-nonnegativity-of-relative-entropy}

This restates Gibbs' Inequality, which the Log Sum Inequality proves more directly. D(p‖q)=∑x∈Xp(x)log⁡p(x)q(x)≥(∑x∈Xp(x))log⁡(∑xp(x)∑xq(x))=1log⁡(11)=0,

with equality if and only if p(x)q(x)=c. Both p and q are probability mass functions, so c=1 (otherwise they wouldn't both sum to 1) and hence we have D(p‖q)=0 if and only if p(x)=q(x) for all x.

◻
from Discrete Entropy
Theorem: Nontrivial intervals are uncountable \@{nontrivial-intervals-are-uncountable}

Every interval in R that contains at least two @distinct elements is uncountable.

from Outer Measure
Theorem: Normal Approximation to the Binomial \@{normal-approximation-binomial}

If X is a binomial random variable with mean μ=np and variance σ2=npq, then

Z=limn→∞X−npnpq=n(z;0,1).

This works well when n is large and p is not extremely close to 0 or 1, and also works well when n is small and p is near 0.5.

Let X be a binomial random variable with parameters n and p. For large n, X has approximately a normal distribution with μ=np and σ2=npq=np(1−p) and

P(X≤x)=∑k=0xb(k;n,p)≈area under normal curve to the left of x+0.5=P(Z≤x+0.5−npnpq)

and the approximation is good if np and n(1−p) are greater than or equal to 5.

Note: Continuity Correction \@{continuity-correction}

The 0.5 is called a continuity correction and comes from the fact that

P(X=k)≈P(k−0.5≤X≤k+0.5).

from Some Continuous Probability Distributions
Theorem: nth root of z \@{nth-root-of-z}

For complex z and integer n, with z=r(cos⁡x+isin⁡x), we have

r1n(cos⁡x+2πkn+isin⁡x+2πkn).

from Algebraic Properties
Theorem: Null Space and Range are Subspaces \@{null-space-and-range-are-subspaces}

Let V and W be vector spaces and let T:V→W be linear. Then the null space and range of T are @subspaces of V and W, respectively.

from Linear Transformations
Theorem \@{open-iff-complement-closed}

A set E is open iff its complement is closed.

Proof \@{proof-of-open-iff-complement-closed}

First, consider the case that Ec is empty, and therefore open. If Ec has no limit points, it is vacuously closed. Suppose Ec has a limit point x. Since E is empty, x must be in Ec, therefore x is closed. Now, consider the case that Ec is empty, and therefore closed. If E is empty, it is open, and the theorem is satisfied. If E is not empty, a point x in E has only points in E in any neighborhood, since all points are in E, and therefore E is open.

Now we deal with the cases where neither E nor Ec are empty.

Now, let Ec be closed. Let x∈E. Since Ec is closed, x is not a limit point of Ec, that is x has some neighborhood that doesn't contain a point in Ec and must therefore be a subset of E. Therefore, x is an interior point of E, and E is open.

Conversely, assume E is open. Let x be a limit point of Ec. Suppose, for the sake of contradiction, that x∈E. Then, since E is open, x is an interior point of E and has some neighborhood that is a subset of E. This is a contradiction, since every neighborhood of x must contain at least one point of Ec to be a limit point of Ec. Therefore, x must be in Ec, and it follows that Ec is closed.

◻
Referenced by (3 direct)

Direct references:

from Metric Spaces
Theorem \@{open-relative-iff-intersection-with-open-subset}

Suppose Y⊂X. A subset E of Y is open relative to Y iff E=Y∩G for some open subset G of X.

Proof \@{proof-of-open-relative-iff-intersection-with-open-subset}

Suppose E is open relative to Y. Then, for every p∈E, there is some rp>0 such that d(p,q)<rp, q∈X implies that q∈Y. Let Vp be the set of all q∈X where d(p,q)<rp (and thus q∈Y) and let

G=⋃p∈EVp.

Then, since each Vp is an open subset of X, so is G. Now, since p∈Vp for each p∈E, E⊂G∩Y. Also, since Vp∩Y⊂E for every p∈E, G∩Y⊂E, and E=G∩Y.

Conversely, suppose E=Y∩G for some open subset G of X. Now, suppose p∈E. Then, p∈G, and there is some neighborhood Vp⊂G. Then, Vp∩Y⊂E, so E is open relative to Y.

◻
Referenced by (1 direct)

Direct references:

from Metric Spaces
Theorem \@{open-set-in-r1-is-countable-union-of-disjoint-segments}

Every open set in R1 is the union of an at most countable union of disjoint segments.

Proof \@{proof-of-open-set-in-r1-is-countable-union-of-disjoint-segments}

Let E be an open set in R1. Let x∈E. Let a=inf{y:(y,x]⊂E} and b=sup{y:[x,y)⊂E}. Then, a<x<b, because E is open and thus x is an interior point of E and there is some neighborhood around x that is entirely within E. Let I(x)=(a,b). By construction, I(x) is connected. For all u∈I(x), I(u) must have the same end points as I(x), since if it extended beyond, our construction of I(x) would be contradicted. Also note that for all v∈E∖I(x), I(v)∩I(x)=∅, for if they intersected, they would form an open interval. Thus, each I(x),x∈E is either disjoint from all others or identical to some other I(y),y∈E, and E is the union of all such unique I.

Now, in each I, we can pick a rational number. Because the rationals are countable, we have at most countably many unique I, and E is their union.

◻
from Perfect Sets and More
Theorem: Orthogonal Decomposition \@{orthogonal-decomposition}

For a,b∈Rn, with b≠0,

a=projba+oprojba.

Referenced by (1 direct)

Direct references:

from Projection
Theorem: Outer measure is translation invariant \@{outer-measure-is-translation-invariant}

Suppose t∈R and A⊂R. Then |t+A|=|A|.

from Outer Measure
Theorem: Outer measure of a closed interval \@{outer-measure-of-a-closed-interval}

Suppose a,b∈R with a<b, Then |[a,b]|=b−a.

Note \@{outer-measure-of-a-closed-interval-note}

The proof for this theorem uses Heine-Borel.

from Outer Measure
Theorem: Outer Measure Preserves Order \@{outer-measure-preserves-order}

Suppose A and B are subsets of R with A⊂B. Then |A|≤|B|.

from Outer Measure
Theorem \@{permutation-as-product-of-disjoint-cycles}

Every permutation σ of a finite set is a product of disjoint cycles.

from Groups
Theorem \@{permutation-parity-is-well-defined}

A permutation in Sn can be written as either a product of an odd number of transpositions or a product of an even number of transpositions, but not both.

from Groups
Theorem \@{permutations-form-group}

Let A be a nonempty set, and SA be the collection of all permutations of A. Then SA is a group under permutation multiplication.

from Groups
Theorem \@{poincare-bendixson}

Suppose that

(1) R is a closed, bounded subset of the plane;

(2) x˙=f(x) is a continuously differentiable vector field on an @open-set containing R;

(3) R does not contain any fixed points;

(4) There exists a trajectory C that is "confined" in R, in the sense that it starts in R and stays in R for all future time.

Then, either C is a closed orbit, or it spirals toward a closed orbit as t→∞. In either case, R contains a closed orbit.

Referenced by (1 direct)

Direct references:

from Limit Cycles
Theorem: Poisson Approximation to the Binomial \@{poisson-approximation-binomial}

Let X be a binomial random variable with probability distribution b(x,n,p). When n→∞, p→0, and limn→∞np=μ remains constant,

limn→∞b(x,n,p)=p(x,μ).

from Some Discrete Probability Distributions
Theorem: Power Rule for Logarithms \@{power-rule-for-logarithms}

TODO: the log of a power moves the exponent out front.

from Logarithms
Theorem \@{probability-vectors-form-a-convex-compact-set}

The set of probability vectors in Rn is a convex set, and it is compact.

Proof \@{proof-of-probability-vectors-form-a-convex-compact-set}

Let E be the set of probability vectors in Rn. That is,

E={p∈Rn:pi≥0,∑i=1npi=1.}

(Note: E is a n−1 dimensional @simplex).

Suppose X,Y∈E. Then

∑i=1nXi=1,∑i=1nYi=1.

Then, let λ∈[0,1]. Now,

∑i=1nλXi=λ,∑i=1n(1−λ)Yi=1−λ,

λX+(1−λ)Y=∑i=1n(λXi+(1−λ)Yi)=λ+1−λ=1.

Since either λ or 1−λ are non-negative, all entries of this convex combination are non-negative, so the combination is again in E and is therefore a probability vector.

We can use Heine-Borel to show that E is compact by showing it is closed and bounded.

Noe that for each p∈E, and each @coordinate i,

{p∈Rn:pi≥0}

is a closed half-space. Now, note that the map

f:Rn→R,f(p)=∑i=1npi

is continuous, the pre-image of 1 under f is

{p∈Rn:∑i=1npi=1.}=f−1({1}).

Because 1 is closed in R, by A mapping f of a metric space... we have that

{p∈Rn:∑i=1npi=1.}

is closed

Now,

E=(⋂i=1n{p:pi≥0})∩{p:∑i=1npi=1}

is an intersection of closed sets, which is also closed.

E is obviously bounded - the sum of all coordinates in p∈E is always 1, so E⊂ the closed ball of radius 1 centered at the origin.

Therefore, E is closed and bounded, and is compact.

TODO: we can generalize this to the fact that @simplexes are convex and compact.

◻
Referenced by (1 direct)

Direct references:

from Markov Chains
Theorem: Product Rule for Logarithms \@{product-rule-for-logarithms}

TODO: the log of a product is the sum of the logs.

Referenced by (1 direct)

Direct references:

from Logarithms
Theorem \@{product-of-convex-sets-is-convex}

Let E⊂Rk and F⊂Rm be convex sets. Then E×F⊂Rk+m is convex.

Proof \@{proof-of-product-of-convex-sets-is-convex}

TODO

◻
Referenced by (1 direct)

Direct references:

from Metric Spaces
Theorem: Pythagorean Theorem \@{pythagorean-theorem}

For orthogonal vectors a,b∈Rn,

‖a‖2+‖b‖2=‖a+b‖2.

Proof \@{proof-of-pythagorean-theorem}

By definition of the @euclidean norm, ‖a+b‖2=⟨a+b,a+b⟩=‖a‖2+2⟨a,b⟩+‖b‖2.Because a and b are orthogonal, their @euclidean inner product is 0, and we have‖a+b‖2=‖a‖2+‖b‖2.

◻
from Projection
Theorem: Quotient Rule for Logarithms \@{quotient-rule-for-logarithms}

TODO: the log of a quotient is the difference of the logs.

from Logarithms
Theorem: Radius of Convergence and Nearest Singularity \@{radius-of-convergence-and-nearest-singularity}

The radius of convergence of the Taylor series for a function f(z) about a point z0 is the distance from z0 to the nearest singularity of f(z).

from Taylor and Maclaurin Series
Theorem: Range is span of transformation of domain basis \@{range-is-span-of-transformation-of-domain-basis}

Let V and W be vector spaces and let T:V→W be linear. If β={v1,v2,…,vn} is a @basis for V, then

R(T)=span(T(β))=span({T(v1),T(v2),…,T(vn)}).

from Linear Transformations
Theorem: Rank Nullity Theorem \@{rank-nullity-theorem}

Let V and W be vector spaces and let T:V→W be linear. If V is @finite-dimensional, then

rank(T)+nullity(T)=dim(V).

from Linear Transformations
Theorem \@{rationals-are-dense-in-reals}

The rationals are dense in the reals.

Proof \@{proof-of-rationals-are-dense-in-reals}

Let x∈R and ϵ>0. Pick n∈N such that 1/n<ϵ. Now, because the reals are Archimedean, for some m∈Z we have that m=⌊nx⌋. Then,

m≤nx≤m+1,mn≤x≤m+1n.

Now, if we let q=mn, we have

0≤x−q<1n<ϵ,

so |x−q|<ϵ. Therefore, every neighborhood of x contains some q∈Q, and so x is either a limit point of Q or else x∈Q, and so the rationals are therefore dense in the reals.

◻
Corollary \@{rational-between-any-two-reals}

If x,y∈R, and x<y, then there exists a p∈Q such that x<p<y. That is, there is always a rational number between any two distinct real numbers.

Proof \@{proof-of-rational-between-any-two-reals}

Pick n∈N such that n(y−a)>1. Because because the reals are Archimedean, there is some k∈Z such that nx<k<ny and x<n/k<y. Thus, q=n/k∈Q and r∈(x,y).

◻
Referenced by (4 direct)

Direct references:

from Real Numbers
Theorem: Real Valued Continuously Differentiable implies Lipschitz Continuous \@{real-valued-continuously-differentiable-implies-lipschitz-continuous}

Suppose f:[a,b]→R is continuously differentiable. Then f is Lipschitz continuous with a Lipschitz constant

L=supx∈[a,b]|f′(x)|.

Proof \@{proof-of-real-valued-continuously-differentiable-implies-lipschitz-continuous}

Because [a,b] is compact and f′ is continuous, by the Extreme Value Theorem we have that f′ attains a minimum and a maximum on [a,b], which gives us L (actually a stronger condition: L=maxx∈[a,b]|f′(x)|=supx∈[a,b]|f′(x)|). By the Mean Value Theorem, for any (x1,x2)⊂[a,b], there exists some c such that f(x2)−f(x1)=f′(c)(x2−x1).The EVT implies that |f′(c)|≤L, so|f(x2)−f(x1)|≤L|x2−x1|, which is what we wanted to show.

◻
from Differentiation
Theorem \@{reals-are-archimedean}

The real numbers are Archimedean.

Referenced by (2 direct)

Direct references:

from Real Numbers
Theorem: Residue Theorem \@{residue-theorem}

Let f(z) be analytic inside a simple closed path C and on C, except for finitely many @singular-points z1,z2,…,zk inside C. Then,

∮Cf(z)dz=2πi∑j=1kResz=zjf(z).

Referenced by (1 direct)

Direct references:

from Residue Integration
Theorem \@{residue-at-mth-order-pole}

Resz=z0f(z)=1(m−1)!limz→z0{dm−1dzm−1[(z−z0)mf(z)]}.

from Residue Integration
Theorem: Reversibility of Markov Chains \@{reversibility-of-markov-chains}

If Random Variables X,Y,Z form a markov chain X→Y→Z, then Z→Y→X is also a Markov Chain (hence it is sometimes written as X↔Y↔Z.)

Proof \@{proof-of-reversibility-of-markov-chains}

Using Bayes' Theorem,

p(x,z|y)=p(x|y)p(z|y)=p(x|y)p(y|z)p(z)p(y). Then,

p(x,y,z)=p(y)p(x|y)p(z|y)=p(y)p(x|y)p(y|z)p(z)p(y).=p(z)p(y|z)p(x|y).

◻
from Markov Chains
Theorem: Row space and nullspace are orthogonal complements \@{row-space-and-nullspace-are-orthogonal-complements}

The row space and nullspace are orthogonal complements. That is,

  • C(A⊤)=N(A)⊥ (orthogonal components in Rn)
  • N(A⊤)=C(A)⊥ (orthogonal components in Rm)

In other words, each x in the nullspace is orthogonal to each row, which comes directly from Ax=0:

Ax=0[(row 1)⋯(row m)][ x ]=[0⋯0]⟵x is orthogonal to row 1 ⟵x is orthogonal to row m

from Matrices
Theorem: Sample Size for Estimating a Mean \@{sample-size-mean}

If x¯ is used as an estimate of μ, we can be 100(1−α)% confident that the error will not exceed a specified amount e when the sample size is

n=(zα/2σe)2.

from Confidence Intervals
Theorem: Sample Size for Estimating a Proportion \@{sample-size-proportion}

If p^ is used as an estimate of p, we can be 100(1−α)% confident that the error will be less than a specified amount e when the sample size is approximately

n=zα/22p^q^e2.

from Confidence Intervals
Theorem: Second Derivative Test for Convexity \@{second-derivative-test-for-convexity}

Let φ be twice differentiable on an open interval (a,b). Then φ is convex on (a,b) if and only if φ″(x)≥0 for all x∈(a,b), and concave if and only if φ″(x)≤0 for all x∈(a,b).

Referenced by (1 direct)

Direct references:

from Convexity
Theorem: Second Simple Pole Residue Formula \@{second-simple-pole-residue-formula}

Resz=z0f(z)=Resz=z0p(z)q(z)=p(z0)q′(z0).

from Residue Integration
Theorem \@{sequence-converges-iff-neighborhood-contains-all-but-finitely-many-points}

{pn} converges to p∈X if and only if every neighborhood of p contains pn for all but finitely many n.

Proof \@{proof-of-sequence-converges-iff-neighborhood-contains-all-but-finitely-many-points}

Suppose {pn} converges to p∈X. Let ϵ>0. For some integer N, d(p,pn)<ϵ when n>N. Therefore, pn∈Bϵ(p) for all but the finitely many pn where n≤N.

Conversely, suppose every neighborhood of p contains all but finitely many pn, i.e., for all but N elements of {pn}. Let ϵ>0. Then, pn∈Bϵ(p) whenever n≥N, therefore, d(p,pn)<ϵ.

◻
Referenced by (3 direct)

Direct references:

from Sequences in Euclidean and Metric Spaces
Theorem \@{sequence-in-compact-metric-space-has-a-convergent-subsequence}

If {pn} is a sequence in a compact metric space X, then some subsequence of {pn} converges to a point in X.

Proof \@{proof-of-sequence-in-compact-metric-space-has-a-convergent-subsequence}

Let E be the range of {pn}. If E is finite, then at least one point p in E must be repeated infinitely many times in {pn}. If we let {ni} be the indices of the occurrences of p in {pn}:

pn1=pn2=⋯=p,

then the subsequence {pni} converges to p.

On the other hand, if E is infinite, then E has a limit point p∈X. Pick n1 so that d(p,pn1<1. Now, after picking n1,…,ni−1, we can pick ni>ni−1 such that d(p,pni)<1/i, so {pni} converges to p.

◻
Referenced by (1 direct)

Direct references:

from Sequences in Euclidean and Metric Spaces
Theorem \@{set-and-closure-have-same-limit-points}

If E is a set in a metric space, then E and E― have the same limit points.

Proof \@{proof-of-set-and-closure-have-same-limit-points}

If E is closed, then we are done, because a set equals its closure if it is closed.

Suppose p is a limit point of E. Then every neighborhood of p contains some q∈E,q≠p. Since q∈E, q∈E―, so p is a limit point of E―.

Conversely, suppose p is a limit point of E―. Then, every neighborhood N of p contains a point of q∈E―,q≠p. If q∈E, then N clearly contains a point in E. Otherwise, q∈E′,qi̸nE. Now, since q∈N and every neighborhood is an open set, q has some neighborhood M⊂N. Since q∈E′, M contains some point s∈E. Since M⊂N, s∈N, and therefore N contains a point in E. Thus, all neighborhoods of p contain some point in E, and p is a limit point of E.

◻
from Metric Spaces
Theorem \@{set-and-its-limit-points-may-have-different-limit-points}

A set E and its limit points E′ do not necessarily have the same limit points.

Proof \@{proof-of-set-and-its-limit-points-may-have-different-limit-points}

Consider P={1n|n∈N}. Then P has one limit point, 0, but P′={0} has no limit points, since the only number that contains 0 in all its neighborhoods is 0 itself (see From this, it's evident that a finite....)

◻
from Metric Spaces
Theorem \@{set-equality-via-subset-inclusion}

Two sets X and Y are equal if and only if X is a subset of Y and Y is a subset of X.

Proof \@{proof-of-set-equality-via-subset-inclusion}

Suppose X and Y are sets with X⊂Y and Y⊂X. Now, suppose x∈X. Then, x∈Y. Conversely, suppose y∈Y. Then y∈X. Thus, (∀x)(x∈X⟺x∈Y), and X=Y.

◻
from Set Theory
Theorem \@{set-is-its-closure-iff-it-is-closed}

If X is a metric space and E⊂X, then

(a) E― is closed.

(b) E=E― iff E is closed.

(c) E―⊂F for every closed set F⊂X such that E⊂F.

By (a) and (c), E― is the smallest closed subset of X that contains E.

Proof \@{proof-of-set-is-its-closure-iff-it-is-closed}

(a) Suppose p∈X and p∉E―. Then p is not in E and is not in E′, and is in fact in E―c. Now, since p is not a limit point of E, it has some neighborhood Nr(p) that does not intersect E. Any point x in Nr(p) is an interior point of Nr(p), and therefore has its own neighborhood Nϵ(x) that does not intersect E, and therefore x is not a limit point of E. Thus, any point in E―c is an interior point of E―c, and E―c is therefore open and its complement, E―, is closed (since a set is open iff its complement is closed.)

(b) Suppose E is closed. Then it contains its limit points, so E=E∪E′=E―. Conversely, suppose E=E―. By (a), E is closed.

(c) Suppose that E⊂F⊂X, and that F is closed. Suppose p∈E―. If p∈E, then p∈F because E⊂F. If p∈E′, then it must be in F also, since F contains all points of E, and is closed, and thus must contain the limit points of E.

◻
Referenced by (2 direct, 1 transitive)

Direct references:

Transitive (depth 1):

from Metric Spaces
Theorem: sigma algebras are closed under countable intersection \@{sigma-algebras-are-closed-under-countable-intersection}

Suppose S is a σ-algebra on a set X. Then

  1. (a) X∈S
  2. (b) if D,E∈S, then D∪E∈S and D∩E∈S and D∖E∈S
  3. (c) if E1,E2,… is a sequence of elements of S, then ⋂k=1∞Ek∈S.
Proof \@{proof-of-sigma-algebras-are-closed-under-countable-intersection}

TODO: full proof from paper notes.

◻
from Measurable Spaces and Functions
Theorem: Simple Poles on the Real Axis \@{simple-poles-on-the-real-axis}

If f(z) has a simple pole at z=a on the real axis, then

limr→0∫C2f(z)dz=πiResz=af(z),

as illustrated below

Principal Value

from Real Integrals
Theorem: smallest sigma algebra containing a collection of subsets. \@{smallest-sigma-algebra-containing-a-collection-of-subsets}

Suppose X is a set and A is a set of subsets of X. Then, the intersection of all σ-algebras on X that contain A is a σ-algebra on X.

Proof \@{proof-of-smallest-sigma-algebra-containing-a-collection-of-subsets}

We know there is at least one σ-algebra on X that contains A because the @power set of X is a @sigma-algebra and contains A.

Now, let S be the intersection of all σ-algebras on X that contain A. Then ∅∈S because by definition of σ-algebra, every σ-algebra contains the empty set. Suppose E∈S. Then E is in every σ-algebra on X that contains A, and by definition, each σ-algebra also contains X∖E, so X∖E∈S. Suppose E1,E2,… is a sequence of elements of S. Then each Ek is in every σ-algebra on X that contains A, and so is the union of these Ek, and so it is in their intersection S as well.

◻
Note \@{smallest-sigma-algebra-containing-a-collection-of-subsets-note}

Smallest makes sense for terminology here because this intersection is a subset of every σ-algebra that contains A.

from Measurable Spaces and Functions
Theorem: Special case of Blaire's theorem \@{baire-category-theorem-special-case}

If Rk=⋃n=1∞Fn, where each Fn is a closed subset of Rk, then at least one Fn has a non-empty interior. Equivalently, If Gn is a dense open subset of Rk, for n=1,2,3,…, then ⋂n=1∞Gn is not empty (in fact, it is dense in Rk.)

Proof \@{proof-of-baire-category-theorem-special-case}

First, note that since Rk=⋃n=1∞Fn, every point in Rk is in some Fn, and so ⋂n=1∞Fnc must be empty.

Suppose, for the sake of contradiction, that no Fn has a non-empty interior, that is, every Fn is closed with an empty interior. Then, each Fnc is open. Moreover, since Fn has an empty interior, it has no points for which there exists a neighborhood that contains only points in Fn, that is, every neighborhood of each point of Fn contains a point in Fnc, so every point in Fn is a limit point of Fnc, and every point in Rk is either in Fnc or is a limit point of Fnc, so each Fnc is non-empty and dense in Rk.

As a base step, let x1 be some point in Rk, and let B1 be an open ball around x1. Since the interior of F1 is empty, B1∩F1c is not empty, and is open.

For the inductive step, suppose we have some Bn that's constructed such that Bn∩Fnc is non-empty and open. Then, we can pick a point xn+1∈Bn∩Fnc,xn+1≠xn, and make a ball Bn+1 around it such that Bn+1⊂Bn∩Fnc, xn∉Bn+1, and Bn+1∩Fn+1c is open and not empty. Now, since Bn+1 satisfies our induction hypothesis, and since B1 does as well, we have Bn defined for all n=1,2,3,….

Since the set of points {xn} is infinite (by induction) and bounded (all points are within B1,) it has a limit point p in Rk.. Now, suppose, for contradiction, that p is not in every Fnc. Then, for some N, p is not in FNc. Since p∉FNc and BN+1⊆FNc, we have p∉BN+1. Since BN+1 is open and p is outside it, p is at some positive distance ε from any point q∈BN+1. But xn∈Bn⊆BN+1 for all n>N, so all these infinitely many points are at distance at least ε from p. Thus any neighborhood of p with radius less than ε contains at most finitely many points of {xn}, contradicting that p is a limit point.

Now, this means that p∈⋂n=1∞Fnc, meaning ⋂n=1∞Fnc≠∅, a contradiction! Therefore, our supposition that every Fn has an empty interior must be incorrect, and some Fn must have a non-empty interior.

◻
from Perfect Sets and More
Theorem: Stationary Distribution of an Ergodic Chain \@{stationary-distribution}

When the markov chain is ergodic, the limit

πk=limn→∞pjk(n)

exists and

∑k=1Nπk=1.

Note \@{stationary-distribution-note}

Here, π=⟨π1,π2,…,πN⟩ and the entries in it represent the long term probabilities of being in any given state, or equivalently, the portion of time spent in any given state.

Note that π⋅P=π, which when combined with the fact that the entries of π sum to 1 lets us solve a linear system of equations to find the entries of π.

Referenced by (1 direct)

Direct references:

from Markov Chains
Theorem: Stoke's Theorem \@{stokes-theorem}

Let S be a @piecewise smooth oriented surface in space and let the boundary of S be a piecewise smooth simple closed curve C. Let F(x,y,z) be a continuous vector function that has continuous first partial derivatives in a domain in space containing S. Then

∬S(curlF)⋅ndA=∮CF⋅r′(s)ds.(2)

Here n is a unit @normal-vector of S. r′=dr/ds is the unit tangent vector and s the arc length of C.

In components, (2) becomes

∬R[(∂F3∂y−∂F2∂z)N1+(∂F1∂z−∂F3∂x)N2+(∂F2∂x−∂F1∂y)N3]dudv=∮C―(F1dx+F2dy+F3dz).

Here, F=[F1,F2,F3],N=[N1,N2,N3],ndA=Ndudv,r′ds=[dx,dy,dz], and R is the region with boundary curve C― in the uv-plane corresponding to S represented by r(u,v).

from Vector Integral Calculus
Theorem: Strong Asymptotic Equipartition Property (Shannon--McMillan--Breiman) \@{strong-asymptotic-equipartition-property-shannon-mcmillan-breiman}

Start with a source of n states a1,…,an, emitted by a @stationary ergodic Markov chain with transition probabilities pik=Pr(Xt+1=ak∣Xt=ai),∑k=1npik=1, and Stationary Distribution of an Ergodic Chain P=(P1,…,Pn). Its entropy rate is, by definition, H=−∑i=1n∑k=1nPipiklog⁡pik. A message is a sequence S=(x1,…,xN) of length N, each xt∈{a1,…,an}. Such a message is a path through the network with probability pS=Px1∏t=1N−1pxtxt+1. Let ϵ,δ>0. Then there exists N0 such that for all N≥N0 the length-N sequences split into two classes:

  1. The typical set, Aδ(N)={S:|1Nlog⁡1pS−H|≤δ}.
  2. The atypical set, Aδ(N)―, with total probability Pr(Aδ(N)―)<ϵ.

Moreover the convergence holds @almost surely: Pr(limN→∞1Nlog⁡1pS=H)=1, so with probability 1 a drawn sequence is typical for all sufficiently large N

Proof \@{proof-of-strong-asymptotic-equipartition-property-shannon-mcmillan-breiman}

--- the left eigenvector solving P=PT for the transition matrix T=(pik) (eigenvalue 1, normalized so ∑iPi=1).

◻
from Entropy of a Discrete Information Source
Theorem \@{subsequential-limits-of-a-metric-space-form-a-closed-set}

The subsequential limits of a sequence {pn} in a metric space X form a closed set subset of X.

Proof \@{proof-of-subsequential-limits-of-a-metric-space-form-a-closed-set}

Let E∗ be the set of all subsequential limits of {pn} and let q be a limit point of E∗. We want to show that q∈E∗.

First, note that if the range of {pn} is just {q}, then q is the only subsequential limit of {pn}. In this case, E∗={q} is a singleton and is closed set, as it vacuously contains all of its limit points. So, assume this is not the case.

Choose n1 so that pn1≠q, and let δ=d(q,pn1). Suppose n1,…,ni−1 are chosen. Since q is a limit point of E∗, there is an x∈E∗ with d(q,x)<δ2i. Since x∈E∗ and is thus the limit (sequence) of some subsequence of {pn}, there is an ni>ni−1 such that d(x,pni)<δ2i. Now, via the triangle inequality,

d(q,pni)≤d(q,x)+d(x,pni)<δ2i+δ2i=2δ2i=δ2i−1,i=1,2,3,….

This means that {pni} converges to q, because we can find a pni as close as desired to q. Therefore q is a subsequential limit of {pn} and so q∈E∗, and E∗ is closed.

◻
Referenced by (1 direct)

Direct references:

from Sequences in Euclidean and Metric Spaces
Theorem: Sum and Difference of Cubes \@{sum-and-difference-of-cubes}

Sum of cubes:

a3+b3=(a+b)(a2−ab+b2)

Difference of cubes:

a3−b3=(a−b)(a2+ab+b2)

from Factoring
Theorem: Sum of Independent Normal Random Variables \@{sum-independent-normal}

If X1,X2,…Xn are independent normal random variables with means μ1,…,μn and variances σ12,…,σn2, then the random variable X1+X2+⋯+Xn is normal with mean μ1+μ2+⋯+μn and variance σ12+σ22+⋯+σn2.

from Joint Probability
Theorem: Sum of Independent Poisson Random Variables \@{sum-independent-poisson}

If X1,X2,…Xn are independent Poisson random variables with parameters λ1,λ2,…,λn, then X1+X2+⋯+Xn is a Poisson random variable with parameter λ1+λ2+⋯+λn.

from Joint Probability
Theorem \@{sums-and-products-of-sequences}

Suppose {sn} and {tn} are complex sequences, and limn→∞sn=s,limn→∞tn=t. Then

(a) limn→∞(sn+tn)=s+t;

(b) limn→∞csn=cs, for any number c;

(c) limn→∞(c+sn)=c+s, for any number c;

(d) limn→∞sntn=st;

(e) limn→∞1sn=1s,sn≠0,s≠0.

Proof \@{proof-of-sums-and-products-of-sequences}

For (a), let ϵ>0, pick Ns such that |sn−s|<ϵ/2 when n≥Ns, and pick Nt such that |tn−s|<ϵ/2 when n≥Nt. Then, let N=max{Ns,Nt}. Then, when n≥N,

|(sn+tn)−(s+t)|=|(sn−s)+(tn−t)|≤|sn−s|+|tn−t|<ϵ.

For (b), If c=0, let ϵ>0, and then |csn−cs|=0<ϵ. Otherwise,

Let ϵ/|c|>0. For some N, when n≥N, we have

|sn−s|<ϵ/|c|⟺|c||sn−s|<ϵ⟺|csn−cs|<ϵ.

For (c), let ϵ>0. For some N, when n≥N, we have

|(sn+c)−(s+c)|=|sn−s|<ϵ.

For (d), first note the identity

sntn−st=(sn−s)(tn−t)+s(tn−t)+t(sn−s).(1)

Now, let ϵ>0. Pick Ns such that |sn−s|<ϵ when n≥Ns, and pick Nt such that |tn−s|<ϵ when n≥Nt. Then, let N=max{Ns,Nt}. Then, when n≥N,

|(sn−s)(tn−t)|<ϵ,

which means

limn→∞(sn−s)(tn−t)=0.

Applying this, along with the results of (a) and (b) to (1) gives:

limn→∞(sntn−st)=limn→∞((sn−s)(tn−t)+s(tn−t)+t(sn−s))=limn→∞(s(tn−t)+t(sn−s))=limn→∞(s(tn−t))+limn→∞(t(sn−s))=s∗0+t∗0=0.

For (e), pick m such that when n≥m,|sn−s|<12|s|, so we have that

|sn−s|<12|s|⟺|sn|+|s|<12|s|⟺|sn|<−12|s|⟺|sn|>12|s|⟺12|sn||s|<1.

Now, let ϵ>0. For some integer N>m, when n≥M, we have that

|sn−s|<12|s|2ϵ.

Thus, when n≥N,

|1sn−1s|=|sn−ssns|=|sn−s||sns|<12|sn||s||s|2ϵ=12|sn||s|ϵ<ϵ.

◻
Referenced by (1 direct)

Direct references:

from Sequences in Euclidean and Metric Spaces
Theorem \@{sup-is-in-closure-of-bounded-nonempty-set-of-reals}

Let E be a nonempty set of real numbers which is bounded above. Let y=supE. Then y∈E―. Hence y∈E if E is closed.

Proof \@{proof-of-sup-is-in-closure-of-bounded-nonempty-set-of-reals}

Suppose y∈E. Then y∈E―. Suppose y∉E. Now, by hypothesis, for every h>0, there is some x such that y−h<x<y, because otherwise, x would be an upper bound on E. Therefore, every neighborhood Nh(y) contains some x∈E, and thus y is a limit point of E and y∈E―.

◻
Referenced by (1 direct)

Direct references:

from Metric Spaces
Theorem: Taylor Expansion Theorem \@{taylor-expansion-theorem}

Let f be analytic in a domain D and z0 be a point in D. Then f can be expanded in a power series

f(z)=f(z0)+f′(z0)(z−z0)+f″(z0)2!(z−z0)2+⋯,

valid in all circles |z−z0|<r containing only points of D.

from Taylor and Maclaurin Series
Theorem \@{theorem-1}

If a function f(z) can be expressed in the form

f(z)=(z−z0)mg(z)

valid in some circle |z−z0|<R, where g(z) is analytic at z0 and g(z0)≠0, then f(z) has a zero of order m at z0.

Intuition \@{theorem-1-intuition}

We can see this from the definition of the taylor series. Assume we're at a zero, that is, that f(z0)=0. Then

f(z)=f(z0)+f′(z0)(z−z0)+f″(z0)2!(z−z0)2+⋯,

and since f(z0) is 0, we're left with all terms that have (z−z0) in them, and so we can factor them out and get

f(z)=(z−z0)(f′(z0)+f″(z0)2!(z−z0)+f″(z0)3!(z−z0)2+⋯.

Now, if f′(z0) does not have a zero at z0, then f′(z0) is not zero and f(z) has a first order zero at z0. If f′(z0) has a zero at z0, we can repeat and move onto the next term until, going through m terms, until we find a term that doesn't have a zero at z0, in which case we will have factored out (z−z0)m and we'll be left with an analytic g(z) with g(z0)≠0.

from Zeros
Theorem \@{theorem-1}

∫02πab−csin⁡θdθ=∫02πab−ccos⁡θdθ=2πab2−c2,b2>c2.

from Real Integrals
Theorem \@{theorem-1}

f^^(ω)=f(−ω).

Proof \@{proof-of-theorem-1}

First we just write the definition: f^^(ω)=12π∫−∞∞12π∫−∞∞f(x)e−ikxdxe−ikωdk

Now we move the outer exponential into the inner integral, which is allowed since it's constant in x.:

f^^(ω)=12π∫−∞∞∫−∞∞f(x)e−ik(x+ω)dxdk

Now we swap the order if integration. We do this in calc 3... some justify it with Fubini's theorem, it's not clear exactly why this is allowed but this is how it goes (TODO: figure this out)

f^^(ω)=12π∫−∞∞∫−∞∞f(x)e−ik(x+ω)dkdx

Now pull out f(x) from the inner integral since it's a constant in k:

f^^(ω)=12π∫−∞∞f(x)∫−∞∞e−ik(x+ω)dkdx

The inner integral is just a delta function:

f^^(ω)=12π∫−∞∞f(x)2πδ(x+ω).dx

Now by, the sifting property of the delta function, this just reduces to

f^^(ω)=f(−ω).

◻
from Fourier Transform
Theorem \@{theorem-1}

The nth roots of unity under multiplication are isomorphic to Zn under addition.

Proof \@{proof-of-theorem-1}

Let

μn={e2piik/n:k=0,1,…,n−1}

be the nth roots of unity, and

Zn={0,1,…,n−1}

be the first n non-negative integers under addition modulo n.

Let

ϕ:Zn→μn,ϕ(k)=e2πik/n

be a mapping we will show to be an isomorphism.

First, note that μn and Zn are obviously the same cardinality, by their definitions.

Now, suppose a,b<n−1. Then

ϕ(a+b)=e2πi(a+b)/n=e2πia/n∗e2πib/n=ϕ(a)∗ϕ(b),

so ϕ is a @group-homomorphism.

Now, eμn is 1, that is, e2πi(0)/n, so ker⁡ϕ=0. But, 0 is eZn, and so ϕ is injective, and an @isomorphism, and μn and Zn are isomorphic.

◻
from Discrete Fourier Transform
Theorem \@{theorem-12}

The only H satisfying the three required properties above is the entropy function defined above, up to multiplication by a constant.

Proof \@{proof-of-theorem-12}

Assume we have a function A(n) that satisfies the three properties listed above, such that

A(n)=H(1n,1n,…,1n).

Then, by property (3) above, we can decompose a choice from sm equally likely possibilities into a sequence of m choices each from s equally likely possibilities. For example, if we have 24 equally likely possibilities, the probability of any given event is 1/16. If we instead we have a series of 4 choices each with 1/2 probability, we end up with 1/16 as the probability of any specific sequence of events. So, we have that A(sm)=mA(s).

Now, with arbitrarily large n, we can also have tn such that A(tn)=nA(t), by the same logic, and we can pick m such that

sm≤tn<sm+1.

Now, we can take the logarithm of each term to get

mlog⁡s≤nlog⁡t<(m+1)log⁡s,

and dividing by nlog⁡s gives

mn≤log⁡tlog⁡s<mn+1n,

and because n is arbitrarily large,

|mn−log⁡tlog⁡s|<ϵ,

where ϵ is arbitrarily small.

By property (2) of A(n) (it is a @monotonically-increasing function of n,)

A(sm)≤A(tn)≤A(sm+1)mA(s)≤nA(t)≤(m+1)A(s).

Then, dividing by nA(s) gives

mn≤A(t)A(s)≤mn+1n or |mn−A(t)A(s)|<ϵ,

Now, by the @triangle-inequality, we have that

|A(t)A(s)−log⁡tlog⁡s|≤2ϵ|A(t)−A(s)log⁡slog⁡t|≤2ϵA(s).

Since ϵ can be arbitrarily small, we have that A(t)=Klog⁡(t), with K>0 so that property (2) holds. Now we know what A(n) is, and thus what H is when we have equal probabilities for all events.

Now let's say that we have a choice from n possible events with commensurable probabilities pi=ni∑ni. We can break down a choice from ∑ni possibilities into a choice from n possibilities with probabilities p1,…,pn and then, if the ith possibility was chosen, ni choices of equal probability pi. We do this because above, we found how to find H when all events are equally likely, and property (3) of our desired function lets us break down our overall choice from ∑ni possibilities. This gives us

Klog⁡∑ni=H(p1,…,pn)+∑piA(ni)=H(p1,…,pn)+∑piKlog⁡ni=H(p1,…,pn)+K∑pilog⁡ni.

Then, H(p1,…,pn)=Klog⁡∑ni−K∑pilog⁡ni=K[log⁡∑ni−∑pilog⁡ni]=K[∑pi(log⁡∑ni)−∑pi(log⁡ni)] because ∑pi=1=K[∑pi(log⁡∑ni−log⁡ni)]=K[∑pi(−log⁡ni∑ni)]=−K∑pilog⁡pi.

If the pi are incommensurable, we can approximate them as closely as we'd like with rationals, since The rationals are dense in the reals.. By the first property we assumed for H, it is continuous in the pi, and so its value at the incommensurable pi equals its limit as we approach via the rationals, and so our expression holds in general. K is left to us to pick, picking it is equivalent to picking a base for the logarithm.

◻
from Discrete Entropy
Theorem \@{theorem-12}

Pairwise independence is strictly weaker than mutual independence.

from Limit Theorems
Theorem \@{theorem-16}

When a random variable is uniformly distributed over an alphabet of n elements, the self-information of any given element equals the entropy of the random variable and is log⁡n.

from Discrete Entropy
Theorem \@{theorem-17}

If a system has a liapunov function, then its fixed point x∗ is globally asymptotically stable: for all initial conditions, x(t)→x∗ as t→∞. Therefore, the system has no closed orbits.

Intuition \@{theorem-17-intuition}

Like gradient systems, we can't get in a loop if we're always moving downhill.

from Limit Cycles
Theorem \@{theorem-19}

Let f(P)=f(x,y,z) be a scalar function having continuous first partial derivatives in some domain B in space. Then, gradf exists in B and is a vector, that is, its length and direction are independent of the particular choice of Cartesian coordinates. If gradf(P)≠0 at some point P, it has the direction of maximum increase of f at P.

Proof \@{proof-of-theorem-19}

The directional derivative of f in the direction of some unit vector u is

Duf=u⋅gradf=|u||gradf|cos⁡θ(a)

where θ is the angle between u and gradf (see The directional derivative of f in the... and The dot product of u and v...). Note that f is a scalar function, as is the directional derivative of f. Now, cosθ has its maximum value of 1 whenever θ=0, and since u is a unit vector with magnitude of 1, (a) simplifies to

Duf=|gradf|,

which tells us that that direction and magnitude of gradf are independent of the coordinate system chosen. Now, since θ=0 if and only if b and gradf are parallel, gradf is the direction of maximum increase of f at P, assuming gradf≠0 at P.

◻
from Vector Differential Calculus
Theorem \@{theorem-19}

Let x˙=f(x) be a continuously differentiable vector field defined on a @simply-connected subset R of the @plane. If there exists a continuously differentiable, @real-valued function g(x) such that ∇⋅(gx˙) has one sign throughout R, then there are no closed orbits lying entirely in R.

from Limit Cycles
Theorem \@{theorem-21}

H=0 iff all the pi but one are zero, this one having the value of one.

Proof \@{proof-of-theorem-21}

Suppose H(p1,…,pn)=0. Then, 0=−∑i=1npilog⁡pi. Note that because 0≤pi≤1, we have log⁡pi≤0, and −pilog⁡pi≥0 (with the convention 0log⁡0=0, since limp→0+plog⁡p=0). Assume for contradiction that more than one pi is non-zero. Then, because ∑pi=1, each non-zero pi is in (0,1) and therefore its −pilog⁡pi>0, and the sum of these terms is therefore non-zero, a contradiction. Now, since all probabilities are required to sum to 1, it can't be the case that all probabilities are zero, which means that exactly one probability must be non-zero and that probability must be 1.

◻
from Discrete Entropy
Theorem \@{theorem-23}

A sequence {pn} converges to p if and only if every subsequence of {pn} converges to p.

Proof \@{proof-of-theorem-23}

Suppose that {pn} converges to p. Suppose some subsequence {pni} converges to q, and suppose, for contradiction, that q≠p. Now, following an argument similar to the proof that limits of sequences are unique, we can see that if p≠q, arbitrary neighborhoods around both can't contain all but finitely many points, so we have a contradiction, and p=q.

Conversely, suppose every subsequence of {pn} converges to p. Then, {pn} is a subsequence of itself, so it converges to p.

◻
from Sequences in Euclidean and Metric Spaces
Theorem \@{theorem-5}

Let bij(s) be the duration of the s-th symbol which is allowable in state i and leads to state j. Then the channel-capacity C is equal to log⁡W where W is the largest real root of the @determinantal-equation

|∑sW−bij(s)−δij|=0,

where δij is the @Kronecker-delta.

from Discrete Entropy
Theorem \@{theorem-50}

Every closed subset E of a complete metric space X is complete.

Proof \@{proof-of-theorem-50}

Let {pn}⊂E be a cauchy sequence. Then, it converges to some point p∈X, and actually p∈E, because E is closed. Therefore, E is complete.

◻
from Sequences in Euclidean and Metric Spaces
Theorem \@{theorem-6}

Let C be a simple, closed piecewise smooth curve, and C1, C2, …, Cn be disjoint, simple, closed piecewise smooth curves in the interior of C. If f is analytic at all points that are both inside or on C, and outside or on each Cj, then

∮cf(z)dz=∑j=1n∮Cjf(z)dz.

from Cauchy-Goursat Theorem
Theorem \@{theorem-7}

Suppose E⊂X, a metric space, p is a limit point of E, f and g are complex functions on E, and

limx→pf(x)=A,limx→pg(x)=B.

Then:

limx→p(f+g)(x)=A+B.

limx→p(fg)(x)=AB.

limx→p(fg)(x)=AB,B≠0.

Proof \@{proof-of-theorem-7}

This follows directly from the that limits of functions are characterized by limits of sequences, and the algebraic properties of sequences of limits.

◻
Remark \@{theorem-7-remark}

If f and g map E into Rk, then (a) remains true, and (b) becomes

limx→p(f⋅g)(x)=A⋅B.

That is, the limit of an inner product of vector valued functions is the inner product of their limits.

(See A sequence in Rk converges iff its components converge).

from Continuity in Euclidean and Metric Spaces
Theorem \@{theorem-7}

If C is a simple, closed, piecewise smooth curve and z0 is interior to C, then:

∮C1z−z0dz=2πi.

Intuition \@{theorem-7-intuition}

See If C is the unit circle, then... and consider path independence and the principle of path deformation. Consider toy contours, particularly a collapsed keyhole contour around the singularity.

from Cauchy-Goursat Theorem
Theorem \@{theorem-7}

Every power series representation of (or, Taylor series for) an entire-function has an infinite radius of convergence.

from Taylor and Maclaurin Series
Theorem \@{theorem-7}

For any Hamiltonian system, H is a conserved quantity.

from Limit Cycles
Theorem \@{theorem-7}

Random variables are mutually independent exactly when their joint distribution is a product distribution.

from Joint Probability
Theorem \@{theorem-9}

If f(1/z) has a singularity at 0, then f(z) has a singularity at the @point-at-infinity.

from Classification of Singularities
Theorem \@{theorem-9}

pjk(m)=Pjkm.

Proof \@{proof-of-theorem-9}

Due to the magic of linear algebra, if we have a row vector x representing the probability of starting in each state, we can compute the probability of ending up in any given state after m steps as

x⋅Pm.

◻
from Markov Chains
Theorem: Total derivatives are unique \@{total-derivatives-are-unique}

Suppose E is an open set in Rn, f:E→Rm, and x∈E, and that A1 and A2 are total derivatives of f at x. Then, A1=A2.

from Vector Differential Calculus
Theorem: Uniform distribution maximizes entropy \@{uniform-distribution-maximizes-entropy}

A random variable has the most entropy when the elements of its alphabet are all equally likely to occur.

Proof \@{proof-of-uniform-distribution-maximizes-entropy}

We will use a @Lagrangian function of entropy to show this. Let

L(p,λ)=−∑i[piln⁡pi]−λ[(∑ipi)−1].

Then, for any pi we want

∂L∂pi=−ln⁡pi−1−λ=0⟹pi=e−1−λ.

But, this means pi doesn't depend on i, and so is the same for each i and therefore pi=1n.

It remains to show that this extreme of H is a maximum. This follows from the facts that the domain is a convex, compact set and that the entropy function is strictly concave. TODO: more details on these.

◻
Referenced by (1 direct)

Direct references:

from Discrete Entropy
Theorem \@{union-and-intersection-of-open-and-closed-sets}

(a) - For any collection {Ga} of open sets, ⋃αGα is open.

(b) - For any collection {Fa} of closed sets, ⋂αFα is closed.

(c) - For any finite collection G1,…,Gn of open sets, ⋂i=1nGi is open.

(d) - For any finite collection F1,…,Fn of closed sets, ⋃i=1nFi is closed.

Proof \@{proof-of-union-and-intersection-of-open-and-closed-sets}

Let G=⋃αGα,x∈G. Then x is in some Gα for some α, and is an interior point of that Gα, since Gα is open. Therefore, x has some neighborhood that is a subset of Gα and therefore of G, so x is an interior point of G and G is open - this shows (a).

Note that

(⋂αFα)c=⋃αFαc,(e)

and by (a) above, (e) is open. Then its complement, ⋂αFα is closed, and we've shown (b).

Now, let x be in G=⋂i=1nGi, so x is in every Gi, and has a neighborhood Ni in every Gi with radius ri>0. Let r be min{r1,…,rn}. Then, x has a neighborhood N of radius r in every Gi, and thus in G, so x is an interior point of G, and we've shown (c).

Now, (⋃i=1nFi)c=⋂i=1nFic is open by (c), so its complement, ⋃i=1nFi is closed, and we've shown (d).

◻
Note \@{union-and-intersection-of-open-and-closed-sets-note}

In parts (c) and (d) of the above theorem, finiteness of the collections of sets is required - the property do not necessarily hold for infinite collections of sets.

Referenced by (9 direct)

Direct references:

from Metric Spaces
Theorem \@{union-of-a-sequence-of-countable-sets-is-countable}

Let {En},n=1,2,3,… be a sequence of countable sets. Then let S=⋃n=1∞En. Then, S is countable.

Proof \@{proof-of-union-of-a-sequence-of-countable-sets-is-countable}

We can construct an infinite array where the rows are sequence constructed by the sets that make up the entries of {En}. Then, we can create a single sequence from all the entries of the sets of {En} by iterating over them in the following order:

sequence = []
for i in range(1, k):
    for j in range(0, i):
        n = i - j
        m = j + 1
        sequence.append(f"E_{n},{m}")

Which, for k=5, yields

E1,1,E2,1,E1,2,E3,1,E2,2,E1,3,E4,1,E3,2,E2,3,E1,4.

This sequence may contain duplicates, so some indices may need to be skipped in constructing a subset T of the positive integers such that T S, but we've now shown that S is at most countable. To show S is infinite and therefore countable, note that the infinite set E1 is a subset of S,, and therefore S is infinite and countable.

◻
Referenced by (1 direct)

Direct references:

from Finite, Countable, and Uncountable Sets
Theorem: Uniqueness of Power Series Expansions \@{uniqueness-of-power-series-expansions}

If f has a power series expansion about a point z0 with nonzero radius of convergence, it must be the Taylor series about z0.

from Taylor and Maclaurin Series
Theorem: Vector Valued Continuously Differentiable implies Lipschitz Continuous \@{vector-valued-continuously-differentiable-implies-lipschitz-continuous}

Suppose f:[a,b]→Rd is continuously differentiable. Then f is Lipschitz continuous with a Lipschitz constant

L≤supx∈[a,b]‖f′(x)‖

where f′ is the Jacobian matrix of f and ‖⋅‖ denotes the matrix norm induced by the @euclidean inner product.

Proof \@{proof-of-vector-valued-continuously-differentiable-implies-lipschitz-continuous}

Because [a,b] is compact and ‖f′‖ is continuous on it, by the Extreme Value Theorem we have that ‖f′‖ attains a minimum and a maximum on [a,b]; then let L=maxx∈[a,b]‖f′(x)‖=supx∈[a,b]‖f′(x)‖. Now, by Mean Value Inequality for Vector Valued Functions, for any (x1,x2)⊂[a,b], there exists some c∈(a,b) such that ‖f(x2)−f(x1)‖≤(x2−x1)‖f′(c)‖. But ‖f′(c)‖≤L, so ‖f(x2)−f(x1)‖≤L|x2−x1|, which is what we wanted to show.

◻
from Differentiation
Theorem: Weak Asymptotic Equipartition Property \@{weak-asymptotic-equipartition-property}

Start with a source alphabet with n symbols a1,…,an, emitted i.i.d. with probabilities p1,…,pn (so pi=Pr(ai)). Its entropy is, by definition,

H=−∑i=1npilog⁡pi.

A message is a sequence S=(x1,…,xN) of length N, each xj∈{a1,…,an}. By independence,

pS=∏j=1NPr(xj)

is the probability of the sequence S being emitted.

Let ϵ,δ>0. Then, there exists N0 such that for all N≥N0, the length-N sequences split into two classes:

  1. The typical set, Aδ(N)={S:|1Nlog⁡1pS−H|≤δ}.
  1. The atypical set, Aδ(N)―, with total probability Pr(Aδ(N)―)<ϵ.

Equivalently, Pr(Aδ(N))→1 as N→∞, i.e. 1Nlog⁡1pS→H in probability.

Proof \@{proof-of-weak-asymptotic-equipartition-property}

First some preliminaries. We have two indices to keep straight here:

  • n - our alphabet size; we use i∈{1,…,n} to index distinct symbols ai, each with its own probability pi.
  • N - sequence length; we use j∈{1,…,N} to index positions in a sequence, each holding some symbol xj.

If we let ci=#{j:xj=ai} be the count of symbol ai in S, so ∑i=1nci=N, then we can restate pS as

pS=∏i=1npici.

ci is the only random thing in pS - it doesn't consider position of symbols, just the total count of each symbol (random) and the probability of that symbol being emitted on any given turn (fixed).

Taking advantage of our symbols being emitted i.i.d., we can convert our expression about the surprisal of the sequence to an equivalent expression about the surprisal of individual symbols being emitted:

1Nlog⁡1pS=1Nlog⁡1∏i=1npici=−1Nlog⁡∏i=1npici=−1N∑i=1nlog⁡pici=−∑i=1nciNlog⁡pi.

This final term is very similar to H=−∑i=1npilog⁡pi; we just need to show that ciN→pi as N→∞. The expected value of ci for N draws is the expected count of ai in N draws, and is

E(ci)=Npi.

So, by the @weak-law-of-large-numbers, ciN→pi as N→∞. That is, 1Nlog⁡1pS=−∑i=1nciNlog⁡pi @converges-in-probability to H as N→∞. This means that for any δ>0,

Pr(|1Nlog⁡1pS−H|>δ)→N→∞0.

That is, that for every ϵ>0, there exists N0 such that for all N≥N0,

Pr(|1Nlog⁡1pS−H|>δ)<ϵ.

That is to say, that the total probability of getting a sequence where the surprisal rate 1Nlog⁡1pS is more than δ from H is less than ϵ for all N larger than some N0, which is what we wanted to show.

◻
Intuition \@{weak-asymptotic-equipartition-property-intuition}

This is just saying that the empirical frequencies in sequences of symbols generated by this source, (c1N,…,cnN) approach the true probabilities for the source distribution, p1,…,pn as N→∞. In other words, the sequences most likely to be produced by the source (typical sequences) are all about equally likely to occur, with probability

pS≐2−HN.

from Entropy of a Discrete Information Source
Theorem: Weierstrass \@{weierstrass}

Every bounded infinite subset of Rk has a limit point in Rk.

Proof \@{proof-of-weierstrass}

Suppose E is a bounded infinite subset of Rk. Then, it is a subset of a k-cell I⊂Rk, and because every k-cell is compact, I is compact. Since infinite subsets of a compact set K have a limit point in K, E has a limit point in I and therefore in Rk.

◻
Note \@{weierstrass-note}

This theorem shows up in other forms, especially related to sequences. For example, in my intro real analysis class, it was expressed as the much weaker "Every bounded sequence in R1 has a convergent subsequence." Other equivalent forms are

  • Any bounded sequence in Rk has a convergent subsequence.
  • Closed and bounded subsets of Rk are sequentially compact.

There seem to be two approaches to topology of metric spaces - the point/set approach used by Rudin and covered here, and a sequence based approach that many other authors like Pugh use in introductory texts. We don't use the term "sequentially compact" anywhere in this page - that's work for a future exercise.

Referenced by (1 direct)

Direct references:

from Compact Sets
Theorem: Well-posedness of IVPs \@{well-posedness-of-ivps}

Consider the IVP

dudt=f(t,u),u(0)=c.

Suppose that f:[0,T]×Rd→Rd is continuous in its domain and Lipschitz continuous in u, i.e., there exists a constant L>0 such that

|f(t,u)−f(t,v)|≤L‖u−v‖,∀(t,u),(t,v)∈[0,T]×Rd.

Then it holds that:

  1. Existence and Uniqueness: There exists a unique solution u(t) for any u0∈Rd.
  2. Continuous Dependence on initial data and right hand side: Suppose r:[0,T]×Rd→Rd is a bounded @perturbation of f, i.e. there exists a constant M>0 such that ‖r(t,u)‖≤M,∀(t,u)∈[0,T]×Rd. Further let u^(t) be the solution of the perturbed IVP du^dt=f(t,u^)+r(t,u^),u^(0)=c^, which we assume exists and is unique. Then we have ‖u(t)−u^(t)‖≤eLt‖c−c^‖+ML(eLt−1),∀t∈[0,T].
from Euler's Method